Complete Inductor Mastery Guide
Master the fundamentals of inductors - from basic concepts and value identification to advanced applications in modern electronics and circuit design
Complete Learning Path - Inductor Fundamentals to Applications
Navigate through comprehensive coverage of inductors from basic principles to advanced applications
What is an Inductor?
An inductor is a passive electronic component that stores energy in a magnetic field when electric current flows through it. Think of it like a magnetic energy reservoir - when current changes, the inductor opposes that change by releasing or absorbing energy, making it essential for filtering, energy storage, and frequency control in electronic circuits.

V = -L × (dI/dt)
Voltage across inductor equals inductance times rate of current change
Why Inductors are Essential
Inductors might seem like simple coils of wire, but they're crucial components that enable many modern electronic functions. Their ability to store magnetic energy and oppose current changes makes them indispensable in power supplies, filters, and RF circuits.
Energy Storage
Inductors store energy in magnetic fields, essential for switching power supplies, boost converters, and energy harvesting circuits.
Filtering
Inductors block AC signals while allowing DC to pass, crucial for power supply filtering and noise reduction in circuits.
Frequency Selection
Combined with capacitors, inductors create resonant circuits for radio tuning, frequency generation, and signal processing.
Current Smoothing
Inductors smooth current flow in power circuits, reducing ripple and providing stable power to sensitive components.
Inductor Symbol and Units
Circuit Symbols
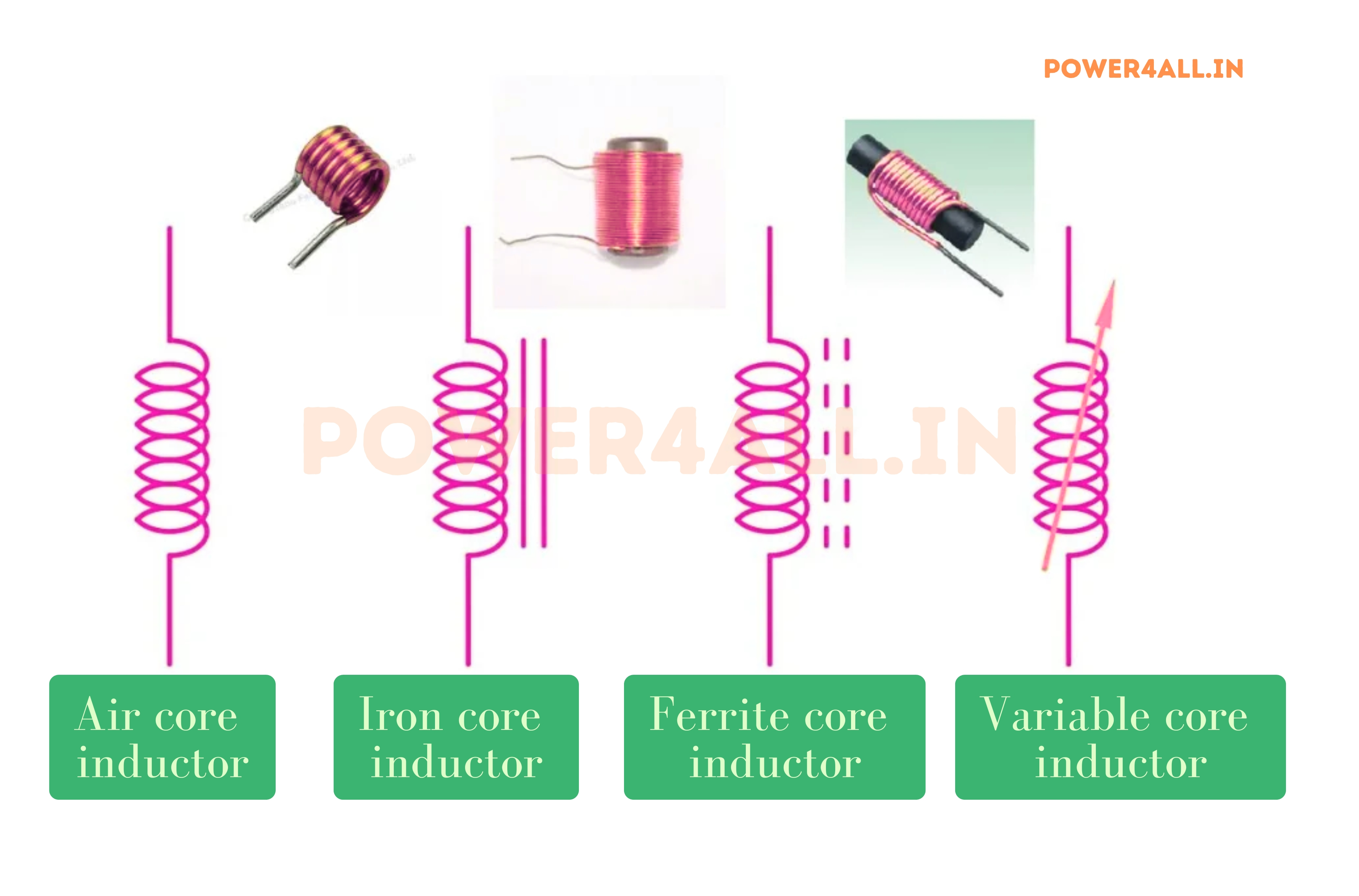
- Air core: Simple coil symbol (curved lines)
- Iron core: Coil with solid line through center
- Ferrite core: Coil with dashed line through center
- Variable inductor: Coil with arrow through it
- Coupled inductors: Two coils with coupling indicator
Units of Measurement
- Henry (H): Basic unit of inductance
- Millihenry (mH): 0.001 henries (most common)
- Microhenry (μH): 0.000001 henries
- Nanohenry (nH): 0.000000001 henries
- Named after: Joseph Henry, American physicist
Everyday Inductor Examples
- Power supply choke: 1mH inductor smooths DC power output
- RF antenna coil: 10μH inductor for radio frequency tuning
- Motor starting inductor: Large inductance for motor current control
- Filter inductor: Removes AC ripple from DC power supplies
- Boost converter: Stores and releases energy for voltage conversion
- Common mode choke: Reduces electromagnetic interference
Did You Know?
The first inductors were discovered by Michael Faraday in the 1830s when he noticed that changing magnetic fields could induce electrical currents. Modern inductors can be smaller than a grain of rice (chip inductors) or larger than a person (power grid inductors), with inductance values ranging from nanohenries to hundreds of henries!
Inductor Fundamentals: How They Work
Understanding how inductors work involves exploring electromagnetic induction, magnetic field theory, and the physical construction that enables energy storage. This knowledge is essential for selecting the right inductor and understanding its behavior in circuits.
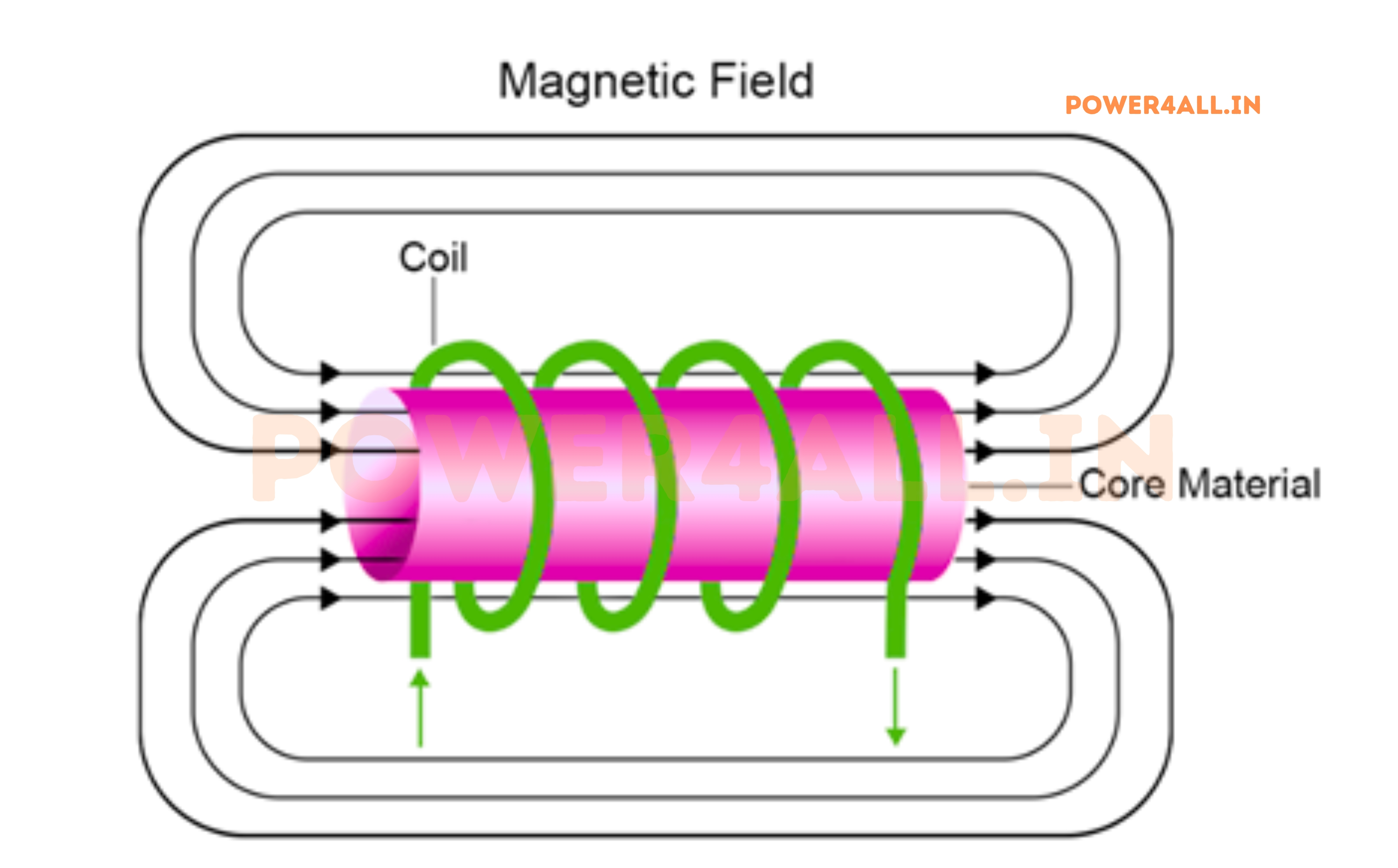
The Physics of Inductance
What Creates Electrical Inductance?
Inductance occurs when current flowing through a conductor creates a magnetic field around it. When this current changes, the changing magnetic field induces a voltage that opposes the current change - this is Lenz's Law in action.
Microscopic View of Inductance
L = μ × N² × A / l
Inductance = Permeability × Turns² × Area / Length
Factors Affecting Inductance
| Factor | Effect on Inductance | Why This Happens | Practical Example |
|---|---|---|---|
| Number of Turns | Squared relationship (N²) | More turns = more magnetic field linking | 10 turns vs 20 turns = 4× inductance |
| Core Material | Dramatic increase with ferromagnetic cores | Higher permeability concentrates magnetic field | Air core vs iron core = 100× difference |
| Coil Area | Direct proportional increase | Larger area captures more magnetic flux | Larger diameter coil = higher inductance |
| Coil Length | Inversely proportional | Longer coil spreads magnetic field | Compact coil vs stretched coil |
Inductor Construction Materials
Air Core Inductors
No magnetic core - wire wound around air space
Construction Details
- Core material: Air (μ = 1, no saturation)
- Wire types: Copper, silver-plated copper, litz wire
- Forms: Ceramic, plastic, or self-supporting
- Inductance range: nH to low mH values
- Advantages: No core losses, high Q factor, linear
- Disadvantages: Large size for high inductance
Applications
- RF circuits: High frequency applications
- Precision filters: No non-linear effects
- Tank circuits: Oscillators and resonant circuits
- Antenna tuning: Radio frequency matching
Iron Core Inductors
Ferromagnetic core for high inductance
Core Materials
- Laminated iron: Thin sheets reduce eddy currents
- Silicon steel: Low loss electrical steel
- Permalloy: Nickel-iron alloy for high permeability
- Amorphous cores: Very low loss modern materials
- Permeability: 100-100,000 times higher than air
- Saturation: Limited by core saturation current
Applications
- Power supplies: Filter chokes and transformers
- Motor drives: Line reactors and filters
- Audio equipment: Low frequency inductors
- Grid applications: Power factor correction
Ferrite Core Inductors
Ceramic magnetic material for high frequency
Ferrite Characteristics
- Material: Iron oxide with other metal oxides
- High resistivity: Reduces eddy current losses
- Frequency range: kHz to GHz applications
- Shapes: Toroids, E-cores, pot cores, rods
- Permeability: 10-10,000 depending on material
- Temperature stable: Good performance over wide temperature range
Common Ferrite Types
- MnZn ferrites: Low frequency, high permeability
- NiZn ferrites: High frequency, lower permeability
- Soft ferrites: Easy magnetization/demagnetization
- Hard ferrites: Permanent magnet applications
Frequency Effects on Inductors
How Frequency Changes Affect Inductor Performance
Inductors behave differently at different frequencies due to parasitic elements, core losses, and skin effect. Understanding these effects is crucial for proper inductor selection.
XL = 2π × f × L
Inductive reactance increases with frequency
Frequency-Dependent Effects
| Effect | Low Frequency | Medium Frequency | High Frequency | Impact |
|---|---|---|---|---|
| Inductive Reactance | Low (ωL small) | Moderate | High (ωL large) | Frequency filtering |
| Wire Resistance | DC resistance | Slightly higher | Much higher (skin effect) | Power loss, Q factor |
| Core Losses | Minimal | Increasing | Significant | Efficiency, heating |
| Parasitic Capacitance | Negligible | Starting to matter | Dominant (self-resonance) | Circuit behavior change |
Self-Resonant Frequency Example
100μH inductor with 5pF parasitic capacitance:
- Resonant frequency: fr = 1/(2π√LC) = 1/(2π√(100×10⁻⁶ × 5×10⁻¹²))
- Calculation: fr = 1/(2π × 2.24×10⁻⁸) = 7.1 MHz
- Below 7.1 MHz: Acts as inductor
- Above 7.1 MHz: Acts as capacitor
- Practical limit: Use below fr/10 ≈ 700 kHz
Types of Inductors: Complete Classification
Inductors come in many different types, each optimized for specific applications, frequency ranges, and performance requirements. Understanding the various types helps in selecting the right inductor for your particular need, whether it's power filtering, RF applications, or precision timing circuits.

Fixed Value Inductors
Through-Hole Inductors
Traditional inductors with leads for PCB mounting
Common Package Types
- Axial leaded: Color-coded like resistors
- Radial leaded: Both leads from one end
- Toroidal: Donut-shaped with wire leads
- Bobbin core: Traditional coil form construction
- Chokes: Large inductors for power applications
Advantages
- Easy to handle and identify
- Higher current capacity
- Good for prototyping
- Replaceable in circuits
- Better heat dissipation
Common Applications
- Power supply filter chokes
- Audio crossover networks
- RF antenna matching circuits
- Motor starting circuits
- Prototype development
Surface Mount Inductors (SMD)
Compact inductors for modern electronics
Standard SMD Sizes
- 0402: 1.0mm × 0.5mm (very low inductance)
- 0603: 1.6mm × 0.8mm (RF applications)
- 0805: 2.0mm × 1.25mm (general purpose)
- 1206: 3.2mm × 1.6mm (higher current)
- 1210: 3.2mm × 2.5mm (power applications)
Construction Types
- Multilayer: Ceramic with printed spirals
- Wire wound: Traditional coil in small package
- Thin film: Deposited metal patterns
- Molded: Wire coil in molded ferrite
Where You Find Them
- Smartphone RF circuits
- DC-DC converter circuits
- EMI filtering applications
- High-density PCB designs
- Automotive electronics
Power Inductors
High current inductors for power applications
Current Ratings and Features
- 1-5 A: Small switching regulators
- 10-20 A: CPU power supplies
- 50+ A: High power converters
- Low DCR: Minimizes power loss
- Saturation current: High current before saturation
Construction Features
- Thick copper wire or foil
- Powder iron or ferrite cores
- Shielded or unshielded options
- Heat sinks or thermal pads
- Low profile packages
Power Applications
- Switching power supplies
- DC-DC buck/boost converters
- LED driver circuits
- Battery charging systems
- Motor drive circuits
Variable Inductors
Adjustable and Variable Inductance Components
Variable Inductors (Variometers)
Inductors with mechanically adjustable inductance values, typically using moving cores or taps on windings.
Slug-Tuned Inductors
- Adjustable core: Ferrite slug moves in/out of coil
- Tuning range: 2:1 to 10:1 inductance variation
- Applications: RF tuning, oscillator adjustment
- Adjustment: Screwdriver or allen key
- Frequency range: kHz to low MHz
Roller Inductors
- Contact roller: Moves along coil length
- Continuous variation: Smooth inductance change
- High Q factor: Low loss connection
- Applications: Antenna tuners, lab equipment
- Range: Wide inductance variation
Switched Inductors
Multiple fixed inductors switched electronically to create variable inductance.
| Type | Switching Method | Speed | Applications |
|---|---|---|---|
| Relay switched | Mechanical relays | Milliseconds | Antenna tuners |
| Semiconductor switched | MOSFETs, PIN diodes | Microseconds | Adaptive filters |
| MEMS switched | Micro-mechanical switches | Microseconds | RF front ends |
Special Purpose Inductors
Toroidal Inductors
Donut-shaped core with excellent magnetic containment
Advantages
- Self-shielding: Magnetic field contained within core
- High efficiency: Minimal flux leakage
- Compact size: Maximum inductance per volume
- Low EMI: Reduced electromagnetic interference
- Linear characteristics: Stable over wide range
Toroidal Applications
- Audio transformers and chokes
- Power supply filters
- Common mode chokes
- Precision measurement equipment
- RF broadband transformers
Common Mode Chokes
Dual winding inductors for EMI suppression
Operating Principle
- Differential signals: Magnetic fields cancel, low impedance
- Common mode noise: Fields add, high impedance
- Core material: High permeability ferrite
- Frequency range: kHz to GHz depending on design
EMI Suppression Applications
- Power line EMI filtering
- USB and data cable filtering
- Switch-mode power supply noise reduction
- Audio system ground loop elimination
- RF interference suppression
RF Inductors
Specialized inductors for radio frequency applications
RF-Specific Requirements
- High Q factor: Low loss at RF frequencies
- Self-resonant frequency: High SRF for operation range
- Temperature stability: Stable over temperature
- Low parasitic capacitance: Minimal inter-winding capacitance
- Tight tolerance: Precise values for tuned circuits
RF Applications
- Antenna matching networks
- Oscillator tank circuits
- RF filter networks
- Impedance matching transformers
- Bias feed inductors
Inductor Value Identification: Reading Inductance Values
Unlike resistors with their standardized color code system, inductors use various marking schemes depending on their type and manufacturer. Learning to identify inductor values is essential for circuit analysis, component replacement, and proper circuit design.
Color Code System (Traditional Inductors)
| Color | Digit Value | Multiplier | Tolerance | Color Sample |
|---|---|---|---|---|
| Black | 0 | ×1 (10⁰) | ±20% | Black |
| Brown | 1 | ×10 (10¹) | ±1% | Brown |
| Red | 2 | ×100 (10²) | ±2% | Red |
| Orange | 3 | ×1,000 (10³) | ±3% | Orange |
| Yellow | 4 | ×10,000 (10⁴) | ±4% | Yellow |
| Green | 5 | ×100,000 (10⁵) | ±0.5% | Green |
| Blue | 6 | ×1,000,000 (10⁶) | ±0.25% | Blue |
| Violet | 7 | ×10,000,000 (10⁷) | ±0.1% | Violet |
| Grey | 8 | ×100,000,000 (10⁸) | ±0.05% | Grey |
| White | 9 | ×1,000,000,000 (10⁹) | - | White |
| Gold | - | ×0.1 (10⁻¹) | ±5% | Gold |
| Silver | - | ×0.01 (10⁻²) | ±10% | Silver |
Reading Color-Coded Inductors
4-Band Reading
Similar to resistor reading but for microhenries (μH)
Band Order (left to right)
Example: 4-Band Reading
Colors: Red, Violet, Brown, Silver
- Red (1st): 2
- Violet (2nd): 7
- Brown (3rd): ×10
- Silver (4th): ±10%
- Result: 27 × 10 = 270μH ±10%
Direct Value Marking
Numerical values printed directly on component
Common Marking Formats
- With units: "100μH", "1.5mH", "47nH"
- Decimal notation: "R47" = 0.47μH, "2R2" = 2.2μH
- Scientific notation: "1005" = 100μH ± 5%
- Code system: Three digits plus tolerance letter
Direct Marking Examples
- "100K": 100μH ±10%
- "221J": 220μH ±5%
- "1R0": 1.0μH
- "R68": 0.68μH
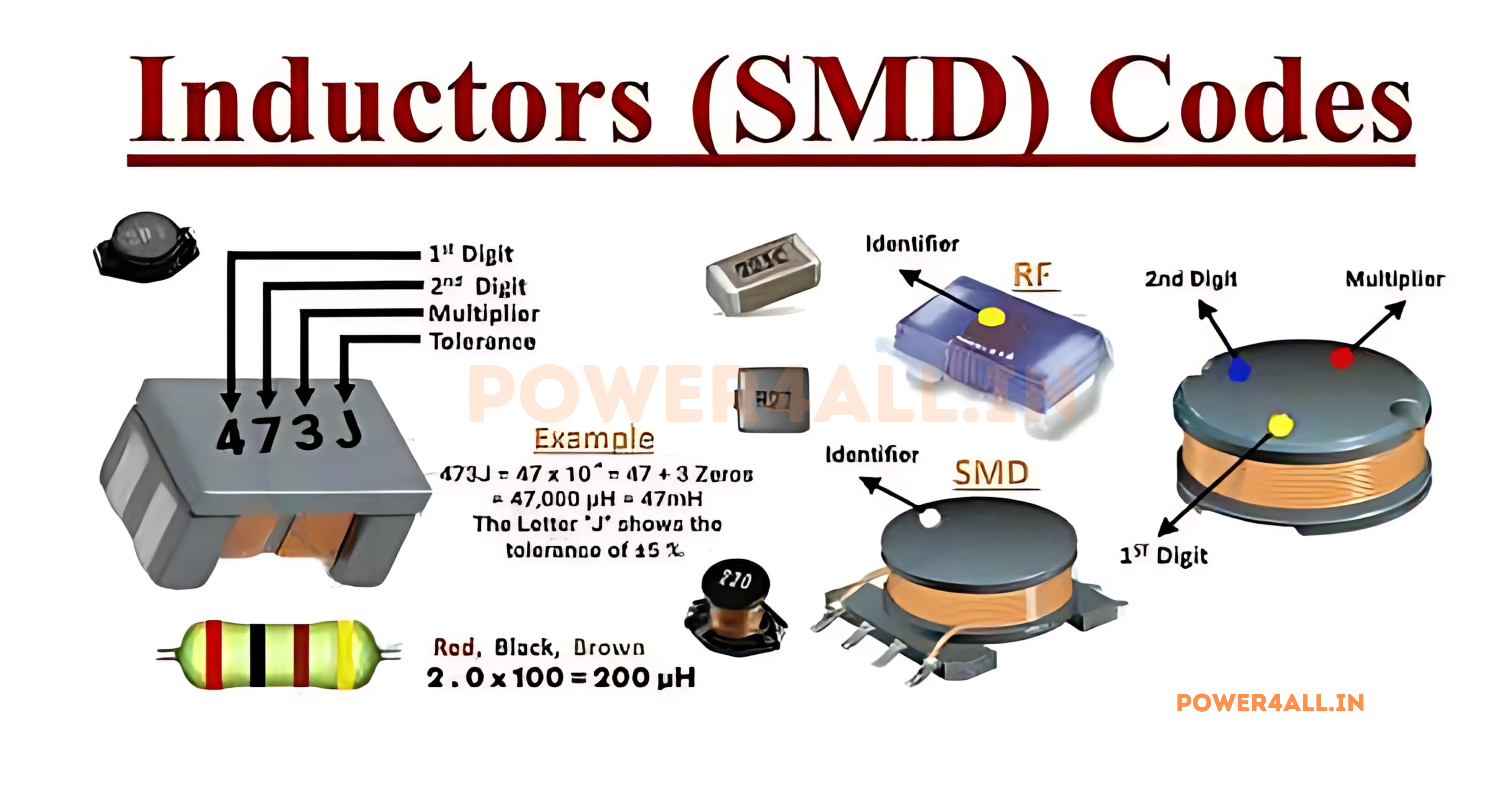
SMD Inductor Marking
Surface Mount Device Value Coding Systems
SMD inductors use various coding systems due to their small size. The marking system varies by manufacturer and component size.
Three-Digit Code System
| Code | First Two Digits | Third Digit (Multiplier) | Value | Unit |
|---|---|---|---|---|
| 101 | 10 | ×10¹ | 100 | nH |
| 221 | 22 | ×10¹ | 220 | nH |
| 102 | 10 | ×10² | 1.0 | μH |
| 472 | 47 | ×10² | 4.7 | μH |
| 103 | 10 | ×10³ | 10 | μH |
Letter Code System
Unit Indicators
R: Decimal point (1R5 = 1.5μH)
N: Nanohenries (N68 = 0.68μH)
K: Microhenries (1K0 = 1.0μH)
Tolerance Codes
J: ±5%
K: ±10%
M: ±20%
No Marking
Very small SMD inductors may have no markings. Value identification requires schematic reference or measurement.
SMD Reading Examples
- "22": Could be 22nH or 0.22μH (check datasheet)
- "1R0K": 1.0μH ±10%
- "N47": 0.47μH
- "101J": 100nH ±5%
- No marking: Requires measurement or schematic reference
Inductance Calculations & Formulas
Understanding inductance calculations is essential for designing circuits with inductors, predicting their behavior at different frequencies, and calculating energy storage. These formulas help in selecting appropriate inductors and understanding their interaction with other circuit elements.
Basic Inductance Relationships
V = L × (dI/dt)
Fundamental inductor voltage-current relationship
Related Formulas
- Energy stored: E = ½ × L × I²
- Reactance: XL = 2π × f × L
- Time constant: τ = L / R
- Resonant frequency: f = 1 / (2π√LC)
Basic Calculation Example
100μH inductor with current changing at 1000 A/s:
- Voltage: V = L × (dI/dt) = 100×10⁻⁶ × 1000 = 0.1V
- At 10kHz: XL = 2π × 10,000 × 100×10⁻⁶ = 6.28Ω
- With 1A current: E = ½ × 100×10⁻⁶ × 1² = 50μJ
Physical Inductance Calculations
Air Core Solenoid
Calculate inductance from physical dimensions
L = (μ₀ × N² × A) / l
Where μ₀ = 4π × 10⁻⁷ H/m
Solenoid Example
100 turns, 1cm diameter, 2cm length:
- Area: A = π × (0.005)² = 7.85×10⁻⁵ m²
- Length: l = 0.02 m
- Inductance: L = (4π×10⁻⁷ × 10000 × 7.85×10⁻⁵) / 0.02
- Result: L = 197 μH
Toroidal Inductor
More complex calculation for toroidal cores
L = (μ × N² × A) / l_path
Where μ = μ_r × μ₀
Toroidal Example
Ferrite core: μ_r = 2000, 50 turns:
- Core area: A = 20×10⁻⁶ m²
- Path length: l = 40×10⁻³ m
- Permeability: μ = 2000 × 4π×10⁻⁷
- Result: L = 1.57 mH
Energy and Power Calculations
Energy Storage in Inductors
Unlike capacitors that store energy in electric fields, inductors store energy in magnetic fields. This energy can be released when the current changes, making inductors essential in switching power supplies.
Energy Calculation Examples
Different scenarios with energy storage:
- 1mH with 1A: E = ½ × 1×10⁻³ × 1² = 0.5 mJ
- 100μH with 10A: E = ½ × 100×10⁻⁶ × 10² = 5 mJ
- 10H with 0.1A: E = ½ × 10 × 0.1² = 50 mJ
- Key insight: Energy increases with the square of current
Series & Parallel Inductor Combinations
Like resistors, inductors can be connected in series and parallel to achieve desired inductance values, current ratings, and circuit characteristics. However, inductors have additional considerations including magnetic coupling, current sharing, and frequency-dependent behavior that make their combination more complex than simple mathematical relationships.
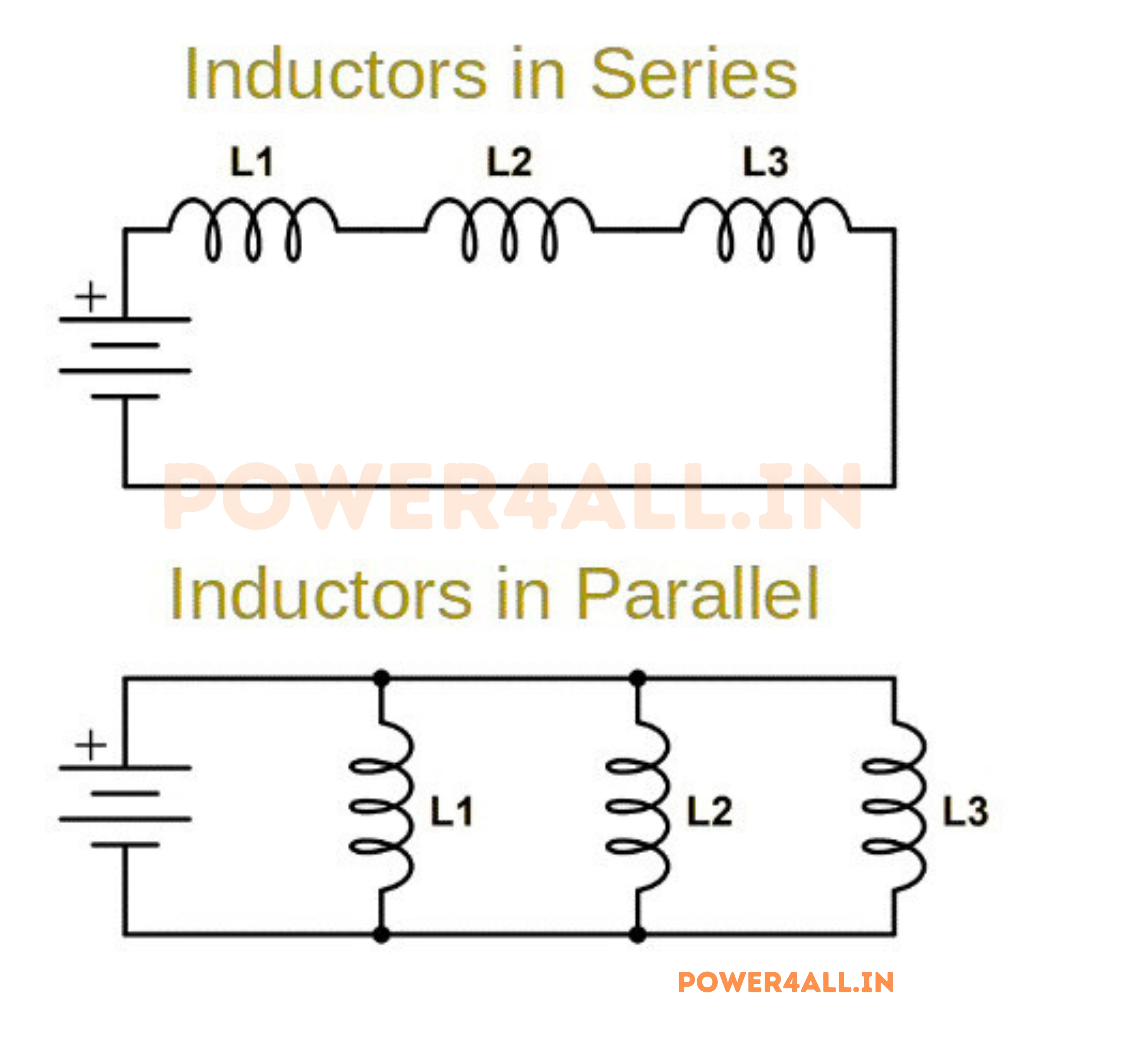
Series Inductor Combinations
Series Connection Principles
In series connections, inductors are connected end-to-end, creating a single current path through all inductors. The magnetic fields can either aid or oppose each other depending on winding polarity.
L_total = L1 + L2 + L3 + ... ± M
Total inductance including mutual inductance effects
Key Characteristics
- Same current: Identical current through all inductors
- Voltage adds: Individual voltages sum algebraically
- Higher total inductance: Sum of individual values (if no coupling)
- Mutual coupling: Can increase or decrease total inductance
Series Calculation Example
Three inductors in series: 100μH, 220μH, 330μH (no coupling):
- Total inductance: 100 + 220 + 330 = 650μH
- Same current: If i = 1A through circuit
- Energy stored: E = ½Li² for each inductor
- E1: ½ × 100×10⁻⁶ × 1² = 50μJ
- E2: ½ × 220×10⁻⁶ × 1² = 110μJ
- E3: ½ × 330×10⁻⁶ × 1² = 165μJ
- Total energy: 50 + 110 + 165 = 325μJ
Mutual Inductance Effects
How Magnetic Coupling Affects Series Combinations
When inductors are placed near each other, their magnetic fields interact through mutual inductance (M). This coupling can significantly affect the total inductance depending on physical arrangement and relative polarity.
Coupling Coefficient
k = M / √(L1 × L2)
Coupling coefficient (0 ≤ k ≤ 1)
| Coupling Type | Coefficient (k) | Series Formula | Effect on Total L |
|---|---|---|---|
| No coupling | k = 0 | L = L1 + L2 | Simple addition |
| Aiding (same polarity) | 0 < k < 1 | L = L1 + L2 + 2M | Increases total L |
| Opposing (opposite polarity) | 0 < k < 1 | L = L1 + L2 - 2M | Decreases total L |
| Perfect coupling | k = 1 | L = (√L1 ± √L2)² | Maximum effect |
Mutual Inductance Example
Two 100μH inductors with k = 0.3 coupling:
- Mutual inductance: M = k√(L1×L2) = 0.3√(100×100) = 30μH
- Aiding connection: L = 100 + 100 + 2×30 = 260μH
- Opposing connection: L = 100 + 100 - 2×30 = 140μH
- No coupling case: L = 100 + 100 = 200μH
- Variation range: 140μH to 260μH depending on polarity
Minimizing Unwanted Coupling
Physical Separation
Increase distance between inductors. Coupling drops with distance cubed for air-core inductors.
Orthogonal Orientation
Mount inductors with axes perpendicular to each other to minimize field interaction.
Magnetic Shielding
Use ferrite shields or mu-metal enclosures to contain magnetic fields.
Toroidal Cores
Self-shielding toroidal inductors minimize external magnetic fields and coupling.
Parallel Inductor Combinations
Parallel Connection Rules
In parallel connections, inductors share common connection points with current dividing between paths based on inductance values and any mutual coupling effects.
1/L_total = 1/L1 + 1/L2 + 1/L3 + ...
Parallel inductance (assuming no mutual coupling)
Key Characteristics
- Same voltage: Identical voltage across all inductors
- Current divides: Inversely proportional to inductance
- Lower total inductance: Always less than smallest individual inductor
- Higher current capacity: Currents add in parallel paths
Parallel Calculation Example
Three inductors in parallel: 300μH, 600μH, 900μH:
- 1/L_total = 1/300 + 1/600 + 1/900
- 1/L_total = 0.00333 + 0.00167 + 0.00111
- 1/L_total = 0.00611
- L_total = 1/0.00611 = 164μH
- Current ratio (at same voltage):
- I1 : I2 : I3 = 1/300 : 1/600 : 1/900
- I1 : I2 : I3 = 6 : 3 : 2
Practical Applications of Combinations
Increased Current Rating
Parallel inductors for higher current applications
Current Sharing Benefits
- Power distribution: Each inductor handles fraction of total current
- Thermal spreading: Heat distributed across multiple components
- Redundancy: Circuit continues if one inductor fails
- Cost effectiveness: Multiple small inductors vs one large inductor
Current Rating Example
Need 100μH inductor with 10A rating:
- Single inductor: Expensive, large, limited availability
- Parallel solution: Four 400μH, 2.5A inductors
- Total inductance: 400μH ÷ 4 = 100μH ✓
- Total current: 4 × 2.5A = 10A ✓
- Advantages: Lower cost, better availability, easier cooling
Custom Inductance Values
Achieving non-standard inductance values
Value Creation Strategies
- Series for higher values: Add inductances together
- Parallel for lower values: Reduce total inductance
- Series-parallel networks: Complex value combinations
- Standard value utilization: Use commonly available values
Custom Value Example
Need 75μH using standard values:
- Option 1: 47μH + 27μH in series = 74μH (close)
- Option 2: 100μH || 300μH = 75μH exactly
- Option 3: Trim 100μH inductor (if variable)
- Best choice: Depends on tolerance, current, cost requirements
Frequency Response Shaping
Complex networks for filter design
Filter Applications
- Multi-stage filters: Series LC sections
- Impedance matching: Complex impedance networks
- Resonant circuits: Series and parallel resonance
- Crossover networks: Audio frequency separation
Audio Crossover Example
2-way speaker crossover at 2kHz:
- Tweeter (high-pass): Series capacitor + parallel inductor
- Woofer (low-pass): Series inductor + parallel capacitor
- Inductor values: Calculate for 8Ω impedance, 2kHz
- L = R/(2πf) = 8/(2π×2000) = 0.64mH
Design Considerations and Limitations
Important Considerations
- Tolerance stacking: Individual tolerances combine in combinations
- Current imbalance: Tolerance differences cause unequal current sharing
- Magnetic coupling: Can significantly alter expected values
- Frequency dependence: Parasitic elements affect high-frequency behavior
- Temperature effects: Different temperature coefficients cause drift
Practical Applications: Inductors in Real Circuits
Inductors serve critical roles in modern electronics, from power management and signal processing to electromagnetic interference suppression and energy storage. Understanding their practical applications helps bridge theoretical knowledge with real-world circuit design and troubleshooting.
Power Supply Applications
Switching Power Supplies
Energy storage and transfer in switch-mode converters
Buck Converter Operation
- Energy storage phase: Switch closed, inductor stores energy
- Energy transfer phase: Switch open, inductor releases energy
- Continuous current: Inductor smooths pulsed current
- Voltage regulation: Duty cycle controls output voltage
L = (Vin-Vout) × D × T / ΔI
Buck converter inductor calculation
Buck Converter Design
12V to 5V, 2A, 100kHz switching:
- Duty cycle: D = Vout/Vin = 5/12 = 0.417
- Allow 20% ripple: ΔI = 0.2 × 2A = 0.4A
- Period: T = 1/100kHz = 10μs
- Inductance: L = (12-5) × 0.417 × 10μs / 0.4A = 73μH
- Standard value: Use 68μH or 82μH
- Current rating: Need >2A saturation, >2A RMS
Boost Converters
Step-up voltage conversion using inductor energy storage
Boost Operation Principle
- Charging phase: Switch closed, inductor charges from input
- Boosting phase: Switch open, inductor voltage adds to input
- Higher output: Output voltage exceeds input voltage
- Continuous mode: Inductor current never reaches zero
LED Driver Application
3.7V battery to 20V for LED string:
- Voltage gain: 20V/3.7V = 5.4×
- Duty cycle: D = 1 - Vin/Vout = 1 - 3.7/20 = 0.815
- High duty cycle: Switch on 81.5% of time
- Inductor stress: High peak currents require careful design
- Applications: LED drivers, PFC circuits, camera flash
Flyback Converters
Isolated power conversion with transformer-inductor
Flyback Characteristics
- Energy storage: Primary inductance stores energy
- Isolation: Transformer provides galvanic isolation
- Multiple outputs: Secondary windings for different voltages
- Discontinuous mode: Energy completely transferred each cycle
Phone Charger Example
120V AC to 5V DC, 2A phone charger:
- Primary inductance: Energy storage during switch-on
- Turns ratio: Determines output voltage
- Gap control: Air gap controls inductance and energy
- Safety isolation: >3kV isolation from mains
- Regulation: Feedback controls primary switching
Signal Processing Applications
Filtering, Resonance, and Signal Conditioning
Low-Pass Filters
Inductors combined with capacitors create effective low-pass filters for removing high-frequency noise and harmonics.
LC Low-Pass Filters
Smooth power supply outputs and audio signals
fc = 1 / (2π√LC)
Cutoff frequency for LC filter
Audio Filter Design
Remove switching noise above 20kHz:
- Target fc = 15kHz (below audio band)
- Choose C = 0.1μF (common value)
- Calculate L = 1/(4π²fc²C)
- L = 1/(4π² × 15000² × 0.1×10⁻⁶) = 1.13mH
- Use standard 1.2mH inductor
- Actual fc = 14.5kHz (acceptable)
Tuned Circuits and Resonance
Frequency selection and oscillator circuits
Series Resonance
- Minimum impedance: XL = XC at resonance
- Maximum current: Limited only by resistance
- Applications: Antenna tuning, filters
- Bandwidth: Determined by Q factor
Parallel Resonance
- Maximum impedance: High impedance at resonance
- Tank circuit: Energy oscillates between L and C
- Applications: Oscillators, IF amplifiers
- Q factor: Higher Q = sharper resonance
RF and Communication Applications
| Application | Frequency Range | Inductor Type | Key Requirements |
|---|---|---|---|
| AM Radio Antenna | 540-1600 kHz | Ferrite rod, variable | High Q, adjustable |
| FM Radio Frontend | 88-108 MHz | Air core, low inductance | Stable, low loss |
| WiFi Filter | 2.4 GHz | Chip inductor, high SRF | Tight tolerance, small size |
| Phone RF Section | 700-2600 MHz | Multilayer, thin film | Ultra-small, high Q |
EMI Suppression and Filtering
Common Mode Chokes
Suppress electromagnetic interference
Operating Principle
- Differential signals: Magnetic fields cancel, low impedance
- Common mode noise: Fields add, high impedance
- Signal preservation: Wanted signals pass through
- Noise suppression: Unwanted noise blocked
USB Cable EMI Filter
Ferrite bead on USB cable:
- Common mode choke: Both data lines through ferrite
- Differential data: Fields cancel, no impedance
- EMI noise: High impedance path, suppressed
- Frequency range: Effective 10MHz-1GHz
- Simple solution: Clip-on ferrite beads
Power Line Filtering
Clean power supply lines and reduce conducted EMI
Filter Configurations
- Series inductors: Block high-frequency noise
- Parallel capacitors: Shunt noise to ground
- Pi filters: C-L-C configuration
- T filters: L-C-L configuration
Switch-Mode Power Supply Filter
Reduce switching noise on output:
- Series inductor: 1-10μH, blocks switching frequency
- Output capacitor: Low ESR, reduces ripple
- Damping resistor: Prevents oscillation
- Result: Clean DC output with minimal ripple
Automotive and Industrial Applications
Automotive Electronics
Applications: Engine control, ABS, airbag systems, infotainment
Requirements: -40°C to +150°C, vibration resistant, EMI immune
Motor Drives
Applications: Variable frequency drives, servo motors, robotics
Requirements: High current, low loss, thermal management
Home Appliances
Applications: Induction heating, microwave ovens, dishwashers
Requirements: Safety certified, cost-effective, reliable
Renewable Energy
Applications: Solar inverters, wind turbines, energy storage
Requirements: High efficiency, grid compliance, long life
Inductor Selection Guide: Choosing the Right Component
Selecting the proper inductor involves balancing multiple parameters including inductance value, current rating, size constraints, frequency performance, and cost. This comprehensive guide walks through the selection process with practical examples and decision trees to help you make informed choices.
Selection Process Overview
Step-by-Step Selection Method
Successful inductor selection requires systematic evaluation of electrical, mechanical, and economic factors in order of importance for your specific application.
Selection Priority Matrix
Typical priority order for different applications:
- Power supplies: Current rating > Size > Cost > Tolerance
- RF circuits: Q factor > SRF > Tolerance > Size
- Audio equipment: Linearity > Q factor > Size > Cost
- Consumer products: Cost > Size > Performance > Features
- Aerospace/Military: Reliability > Performance > Environment > Cost
Testing & Troubleshooting Inductors
Proper testing and troubleshooting of inductors requires understanding their behavior under different conditions and using appropriate measurement techniques. This section covers testing methods, common failure modes, diagnostic procedures, and practical troubleshooting strategies.
Measurement Techniques
Basic Inductance Measurement
Using LCR meters and multimeters
LCR Meter Measurements
- Test frequency: Choose appropriate frequency (100Hz-1MHz)
- Test signal level: Use specified test voltage/current
- DC bias: Some meters can apply DC bias
- Temperature: Measure at operating temperature
- Quality factor: Simultaneous L and Q measurement
LCR Meter Setup
Testing 100μH power inductor:
- Test frequency: 1kHz (below switching frequency)
- Test signal: 0.1V RMS (low level)
- DC bias: 50% of rated current if available
- Expected reading: 80-120μH (±20% tolerance)
- Q factor: Should be >20 for good quality
Saturation Current Testing
Determining actual saturation characteristics
Test Setup Requirements
- DC current source: Variable, high current capability
- LCR meter with bias: Measures L vs DC current
- Current monitoring: Accurate current measurement
- Temperature control: Heat sinking or thermal chamber
Isat = I at (L = 0.8 × L₀)
Saturation current at 20% inductance drop
Saturation Test Procedure
- Measure initial inductance L₀ at zero DC bias
- Apply increasing DC current in steps
- Measure inductance at each current level
- Plot L vs I characteristic curve
- Find current where L drops to 80% of L₀
- Compare with datasheet specification
Thermal Testing
Validating thermal performance and current ratings
Temperature Rise Testing
- Thermocouple placement: Hottest point on inductor
- Current source: Constant RMS current
- Ambient control: Controlled environment chamber
- Steady state: Wait for thermal equilibrium
- Safety monitoring: Temperature limits and alarms
Current Rating Verification
Testing 3A RMS inductor:
- Test current: 3A RMS constant current
- Ambient: 25°C controlled temperature
- Monitor: Core and winding temperatures
- Acceptance: Temperature rise <40°C
- Duration: 2+ hours for steady state
Common Failure Modes
Understanding How Inductors Fail and Why
Electrical Failures
| Failure Mode | Symptoms | Root Causes | Detection Method |
|---|---|---|---|
| Open Circuit | No continuity, infinite resistance | Wire breakage, thermal stress, overcurrent | Resistance measurement |
| Short Circuit | Very low inductance, low resistance | Turn-to-turn shorts, insulation breakdown | Inductance and resistance measurement |
| Core Saturation | Reduced inductance under load | Excessive DC current, inadequate core | L vs I curve measurement |
| High DCR | Excessive power loss, heating | Poor wire joints, corrosion | DC resistance measurement |
| Parametric Drift | Value outside tolerance | Aging, temperature cycling, stress | Precision L measurement |
Mechanical Failures
Core Cracking
Causes: Thermal shock, mechanical stress, vibration
Effects: Reduced inductance, increased losses
Detection: Visual inspection, inductance measurement
Wire Fatigue
Causes: Vibration, thermal cycling, flexing
Effects: Intermittent opens, high resistance
Detection: Resistance vs temperature testing
Thermal Damage
Causes: Overcurrent, poor heat dissipation
Effects: Wire insulation failure, core damage
Detection: Visual discoloration, smell
Failure Analysis Case Study
Power supply inductor failure in automotive application:
- Symptom: Switching regulator instability, audible noise
- Initial test: Inductance measured 40% low
- Further investigation: High DCR, discolored core
- Root cause: Thermal cycling caused wire fatigue
- Solution: Better thermal design, higher rated inductor
Diagnostic Procedures
Systematic Diagnosis
Step-by-step troubleshooting approach
In-Circuit Testing
Testing inductors without removal from circuit
In-Circuit Limitations
- Parallel paths: Other components affect measurements
- DC bias: Circuit may provide DC bias current
- Signal injection: May disturb circuit operation
- Safety considerations: High voltage, stored energy
In-Circuit Safety
Always power down circuits and discharge energy storage elements before testing. Use isolation transformers and appropriate PPE when working with high voltage circuits.
Required Test Equipment
Essential tools for inductor testing and diagnosis
Basic Test Equipment
- Digital multimeter: DC resistance, continuity
- LCR meter: Inductance, Q factor, ESR
- Oscilloscope: Waveform analysis, ripple measurement
- Function generator: AC signal injection
- DC power supply: Bias current, saturation testing
Advanced Equipment
- Impedance analyzer: Frequency response characterization
- Thermal camera: Hot spot identification
- Network analyzer: S-parameter measurement
- Current source: High current bias capability
Troubleshooting Common Circuit Problems
| Circuit Problem | Possible Inductor Issues | Diagnostic Tests | Solutions |
|---|---|---|---|
| Switching regulator instability | Saturation, wrong value, core losses | L vs I curve, ripple measurement | Higher saturation current, different core |
| Excessive ripple current | Too low inductance, high DCR | Inductance verification, DCR test | Higher inductance value, lower DCR |
| Audible noise | Magnetostriction, loose core | Visual inspection, frequency analysis | Different core material, mechanical fix |
| EMI problems | Poor shielding, high SRF | EMI scan, impedance measurement | Shielded inductor, additional filtering |
| Poor efficiency | High core losses, high DCR | Power measurement, thermal analysis | Low loss core, larger wire gauge |
Troubleshooting Example: DC-DC Converter
Problem: Buck converter output voltage unstable, efficiency poor
- Initial observation: Output voltage varies with load
- Ripple measurement: Excessive current ripple (>50%)
- Inductor test: Measured 30μH vs 100μH nominal
- Saturation test: Inductance drops at 2A vs 5A rating
- Root cause: Inductor saturating under normal load
- Solution: Replace with higher saturation current inductor
- Verification: Stable output, ripple within specification
Safety Considerations: Working Safely with Inductors
Inductors can present unique safety challenges due to their energy storage capabilities, high voltages during switching, and potential for generating dangerous back-EMF. Understanding these hazards and implementing proper safety measures is essential for safe design, testing, and maintenance of inductor-based circuits.
Energy Storage Hazards
Critical Safety Warning
Large inductors can store significant magnetic energy that converts to extremely high voltages when current is suddenly interrupted. This can cause electric shock, component damage, or arc flash. Always use proper disconnection procedures and safety equipment.
Back-EMF Generation
High voltages from current interruption
The Physics of Back-EMF
- Lenz's Law: Inductor opposes current changes
- Voltage magnitude: V = L × (dI/dt)
- Fast switching: High dI/dt creates dangerous voltages
- Arc formation: Can exceed breakdown voltage of air
Back-EMF Calculation
1H inductor with 10A suddenly disconnected in 1μs:
- Rate of change: dI/dt = 10A / 1×10⁻⁶s = 10⁷ A/s
- Back-EMF: V = 1H × 10⁷ A/s = 10,000,000V = 10MV!
- Reality: Arc formation limits actual voltage
- Danger: Still thousands of volts possible
- Protection needed: Proper disconnection methods
Stored Energy Calculations
Understanding energy storage capacity
E = ½ × L × I²
Energy stored in magnetic field (Joules)
| Inductor | Current | Stored Energy | Hazard Level |
|---|---|---|---|
| 100μH, 1A | 1A | 50μJ | Minimal |
| 1mH, 10A | 10A | 50mJ | Moderate - can damage components |
| 1H, 1A | 1A | 0.5J | High - can cause shock |
| 1H, 10A | 10A | 50J | Dangerous - potentially lethal |
Protection Methods
Safe disconnection and protection techniques
Flyback Diodes
- Function: Provide current path when circuit opens
- Placement: Across inductor, reverse biased during normal operation
- Rating: Must handle full inductor current
- Speed: Fast recovery diodes for switching circuits
Snubber Circuits
- RC snubbers: Resistor-capacitor to limit voltage rate
- TVS diodes: Transient voltage suppressors
- MOV protection: Metal oxide varistors for high energy
- Active clamping: Electronic circuits for precise control
Thermal Safety
Heat-Related Hazards and Fire Prevention
Temperature Hazards
Burn Hazards
Power inductors can reach temperatures exceeding 150°C during normal operation. Skin contact can cause severe burns within seconds.
Fire Risk
Overheated inductors can ignite nearby flammable materials, especially paper, plastic insulation, or cleaning solvents.
Component Damage
Excessive heat can damage nearby components, cause solder joints to fail, or delaminate PCB materials.
Thermal Protection Strategies
| Protection Method | Application | Trigger Temperature | Response |
|---|---|---|---|
| Thermal fuses | Power supplies | 85-200°C | Permanent shutdown |
| Thermistors | Motor drives | Adjustable | Electronic shutdown |
| Thermal switches | Industrial systems | 40-150°C | Reversible cutoff |
| Software monitoring | Smart systems | Programmable | Controlled deration |
Fire Safety Guidelines
- Keep Class C fire extinguishers nearby when working with electrical equipment
- Never use water on electrical fires - use CO2 or dry chemical extinguishers
- Install smoke detectors in areas with high-power inductor equipment
- Maintain clear evacuation paths and emergency lighting
- Regular inspection of high-temperature components and their surroundings
Frequently Asked Questions About Inductors
Here are the most common questions about inductors, covering everything from basic concepts to practical applications. These answers help clarify common misconceptions and provide practical guidance for working with inductors.
Basic Concept Questions
Q: What's the difference between inductors and capacitors?
A: Inductors and capacitors are complementary components that store energy in different ways:
| Characteristic | Inductor | Capacitor |
|---|---|---|
| Energy Storage | Magnetic field (E = ½LI²) | Electric field (E = ½CV²) |
| Opposes Changes In | Current | Voltage |
| DC Behavior | Acts like short circuit (low resistance) | Acts like open circuit (no current) |
| AC Behavior | Impedance increases with frequency | Impedance decreases with frequency |
| Phase Relationship | Current lags voltage by 90° | Current leads voltage by 90° |
Q: Do inductors in parallel add like resistors?
A: No, inductors in parallel combine using the reciprocal formula, just like resistors in parallel:
1/L_total = 1/L1 + 1/L2 + 1/L3 + ...
Parallel inductance formula
Quick Summary
- Series inductors: Add directly (L_total = L1 + L2 + L3...)
- Parallel inductors: Use reciprocal formula (like parallel resistors)
- Series capacitors: Use reciprocal formula
- Parallel capacitors: Add directly
Q: Why do inductors behave differently with DC vs AC?
A: Inductors respond to the rate of current change, not the current level itself:
- DC (steady current): No current change (dI/dt = 0), so voltage across inductor is zero. Inductor acts like a short circuit with only wire resistance.
- AC (changing current): Continuous current change creates voltage across inductor. Higher frequency = faster change = higher voltage = higher impedance.
- Sudden changes: Fast current changes (like switching) create large voltage spikes that can damage components.
V = L × (dI/dt)
Voltage depends on rate of current change
Practical Application Questions
Q: How do I choose an inductor for a switching power supply?
A: Switching power supply inductor selection involves several key parameters:
Key Design Rules
- Keep current ripple between 10-30% of output current
- Use saturation current rating at least 1.2× peak current
- Choose core material appropriate for switching frequency
- Consider shielded inductors to minimize EMI
Q: Why does my inductor stop working at high frequencies?
A: Inductors have a self-resonant frequency (SRF) above which they behave more like capacitors than inductors:
What Happens at High Frequencies:
- Parasitic capacitance: Inter-winding capacitance becomes significant
- Self-resonance: Inductance resonates with parasitic capacitance
- Above SRF: Component acts capacitive, not inductive
- Core losses: Increase dramatically with frequency
- Skin effect: Wire resistance increases due to current crowding
Solutions for High-Frequency Operation
- Choose inductors with high SRF: Use smaller, air-core, or specialty RF inductors
- Operate well below SRF: Rule of thumb: use frequency <1/5 of SRF
- Use appropriate core materials: Air core for highest frequency, ferrite for medium frequency
- Consider chip inductors: Lower parasitic capacitance than wire-wound types
Q: How do I measure inductance without an LCR meter?
A: Several methods can measure inductance using common equipment:
Method 1: Resonance Method
Method 2: AC Impedance Method
Accuracy Limitations
These methods provide approximate values suitable for basic verification. For precision measurements, invest in a quality LCR meter or impedance analyzer.
Troubleshooting Questions
Q: How do I know if my inductor has failed?
A: Inductor failures can be detected through several symptoms and tests:
Common Failure Symptoms:
Open Circuit
Symptoms: No continuity, circuit doesn't function
Test: Measure DC resistance - should be low ohms, not infinite
Shorted Turns
Symptoms: Reduced inductance, increased current
Test: Measure inductance - will be significantly lower than rated
Overheating
Symptoms: Discoloration, smell, performance drift
Test: Visual inspection, thermal imaging, parameter measurement
Core Saturation
Symptoms: Reduced inductance under load, audible noise
Test: Measure inductance vs. DC current characteristic
Quick Diagnostic Procedure
- Visual inspection: Look for burns, cracks, discoloration
- Continuity test: Should have low resistance (typically <1Ω)
- Inductance measurement: Should be within tolerance of rated value
- In-circuit behavior: Check if circuit operates as expected
- Thermal check: Operating temperature should be reasonable
Conclusion: Mastering Inductor Technology
Congratulations! You've completed a comprehensive journey through the world of inductors, from fundamental physics to advanced applications. This knowledge foundation will serve you well in designing, troubleshooting, and optimizing electronic circuits across many fields.
Key Takeaways
Fundamental Understanding
Inductors store energy in magnetic fields and oppose changes in current. This simple concept enables complex applications from power conversion to signal processing.
Material Matters
Core materials determine inductor performance: air cores for linearity, ferrite for efficiency, iron for high inductance. Choose based on your application needs.
Design Calculations
Proper inductor selection requires calculating inductance values, current ratings, power dissipation, and thermal management for reliable operation.
Safety First
Inductors can store dangerous amounts of energy and generate high voltages. Always follow proper safety procedures and use appropriate protection circuits.
Congratulations!
You now have a solid foundation in inductor theory and practice. Remember that mastery comes through continued learning and practical application. Use this knowledge responsibly and always prioritize safety in your designs and experiments.