Master Kirchhoff's Laws
Complete guide to Kirchhoff's Current Law (KCL) and Voltage Law (KVL) - the fundamental principles of circuit analysis that every electronics engineer must know
Complete Learning Path - Kirchhoff's Laws Fundamentals to Applications
Navigate through comprehensive coverage of Kirchhoff's Laws from basic principles to advanced applications
Introduction to Kirchhoff's Laws
Kirchhoff's Laws are the cornerstone of electrical circuit analysis, providing the mathematical foundation for understanding how current flows and voltage distributes in any electrical network. Named after German physicist Gustav Kirchhoff who formulated them in 1845, these laws are based on fundamental physical principles and are essential for every electronics engineer, student, and hobbyist.
Why These Laws Matter
Before Kirchhoff's Laws, analyzing electrical circuits was largely empirical and limited to simple configurations. These laws transformed circuit analysis into a systematic, mathematical discipline that allows engineers to predict and control electrical behavior with precision.
Historical Impact
- 1845: Gustav Kirchhoff publishes his circuit laws
- Telegraph Era: Enabled long-distance communication networks
- Power Systems: Foundation for electrical grid design
- Modern Electronics: Basis for all circuit design software
- Today: Essential for smartphones, computers, and IoT devices
The Physical Foundation
Kirchhoff's Laws aren't arbitrary mathematical rules - they're direct consequences of fundamental physics principles that govern our universe.
Conservation of Charge
Electric charge cannot be created or destroyed in a circuit. This fundamental principle directly leads to Kirchhoff's Current Law.
Conservation of Energy
Energy supplied by sources must equal energy consumed by loads. This energy balance principle gives us Kirchhoff's Voltage Law.
Universal Application
These laws apply to all circuits - DC, AC, linear, nonlinear, simple or complex. They're truly universal principles.
Mathematical Precision
Transform complex circuit problems into solvable systems of equations, enabling computer-aided design and analysis.
Learning Approach
This guide is designed for complete beginners. We'll start with simple concepts and gradually build to advanced applications. Each law will be explained with intuitive analogies, clear mathematics, and practical examples you can try at home.
What are Kirchhoff's Laws?
Kirchhoff's Laws consist of two fundamental principles that describe the behavior of electric current and voltage in circuits. These laws provide the mathematical tools needed to analyze any electrical network, no matter how complex.
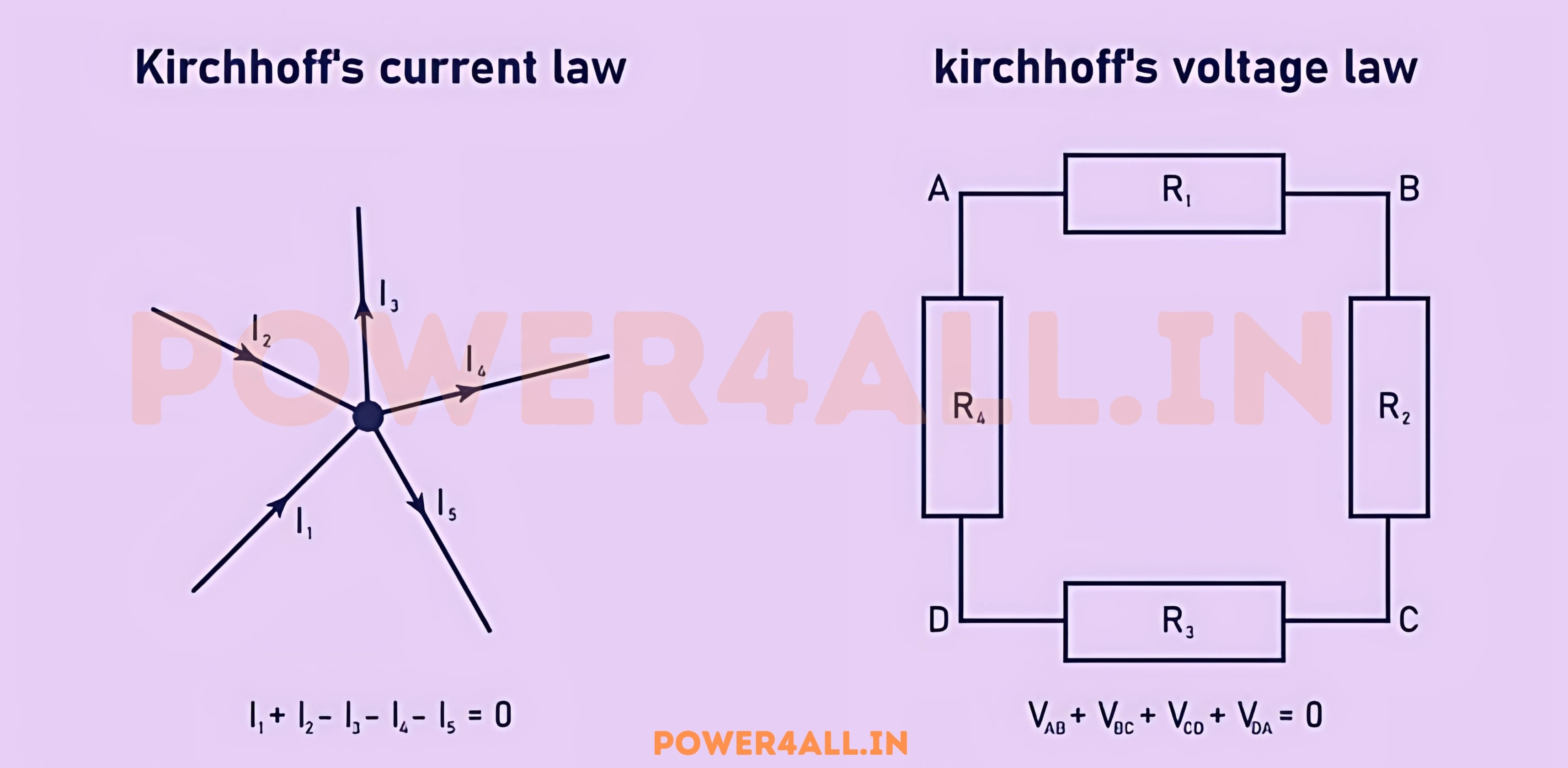
The Two Fundamental Laws
Kirchhoff's Current Law (KCL)
Also known as: Kirchhoff's First Law, Junction Rule, or Node Law
ΣI_in = ΣI_out
Current entering = Current leaving
Simple Explanation
At any junction (node) in a circuit, the total current flowing in must equal the total current flowing out. Think of it like water at a pipe junction - water flowing in equals water flowing out.
Why This Happens
- Based on conservation of electric charge
- Charge cannot accumulate at a junction
- What goes in must come out
Kirchhoff's Voltage Law (KVL)
Also known as: Kirchhoff's Second Law, Loop Rule, or Mesh Law
ΣV = 0
Sum of voltages around any loop = 0
Simple Explanation
If you start at any point in a circuit and trace around any closed loop, adding up all voltage rises and drops, the total will always be zero. It's like hiking - if you start and end at the same elevation, your net elevation change is zero.
Why This Happens
- Based on conservation of energy
- Energy supplied = Energy consumed
- No net energy gain around a closed path
Intuitive Analogies
Understanding Through Everyday Examples
Water Flow Analogy (KCL)
Imagine a water pipe system with a junction where one large pipe splits into three smaller pipes.
Key Insight
Water can't magically appear or disappear at the junction, just like electric current can't accumulate at a circuit node.
Hiking Elevation Analogy (KVL)
Think of voltage as elevation and current as a hiker walking around a circular trail.
Mathematical Check:
+500ft - 200ft - 300ft = 0 ✓ (KVL satisfied)
When and Where to Apply Each Law
| Law | Apply When | Apply Where | Gives You | Common Use |
|---|---|---|---|---|
| KCL | Analyzing current distribution | At circuit nodes/junctions | Unknown currents | Node voltage analysis |
| KVL | Analyzing voltage distribution | Around closed loops | Unknown voltages | Mesh current analysis |
| Both | Complex circuit analysis | Throughout the circuit | Complete solution | General circuit analysis |
Important Note
While these laws might seem simple, they're incredibly powerful. Every circuit analysis software, from SPICE to modern simulators, uses these laws as their foundation. Master these, and you master circuit analysis!
Kirchhoff's Current Law (KCL) - Complete Guide
Kirchhoff's Current Law states that the algebraic sum of currents entering and leaving any node in a circuit equals zero. This law is the mathematical expression of charge conservation and is fundamental to understanding how current distributes in electrical networks.
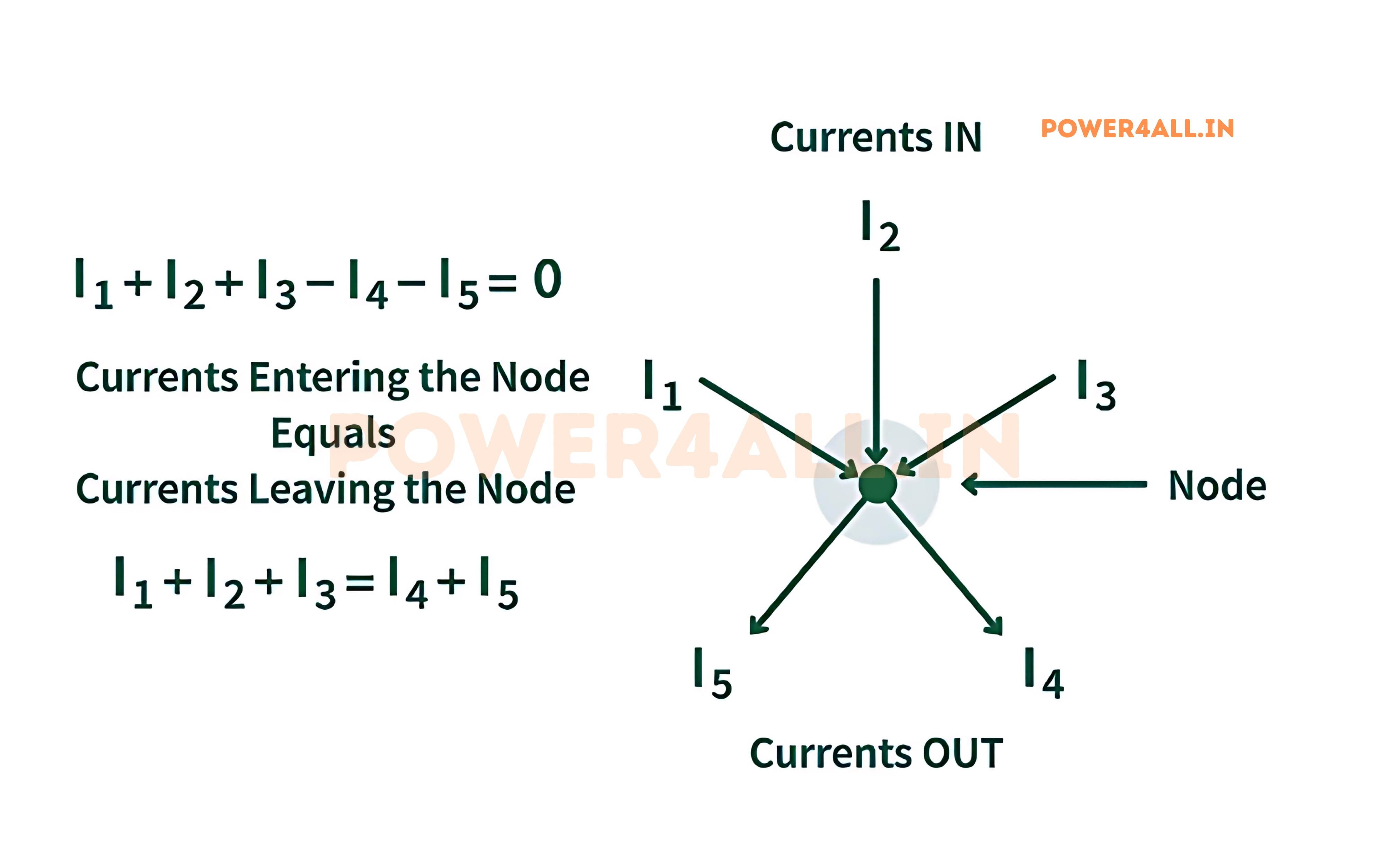
Mathematical Formulation
∑I = 0
Algebraic sum of all currents at a node
Alternative Forms
- ∑I_in = ∑I_out (Sum of currents in = Sum of currents out)
- I₁ + I₂ + I₃ + ... + Iₙ = 0 (Algebraic sum form)
- ∑I_entering - ∑I_leaving = 0 (Sign convention form)
Sign Convention
Choose a consistent sign convention:
- Method 1: Entering currents = positive, Leaving currents = negative
- Method 2: All currents toward node = positive, Away from node = negative
- Key: Be consistent throughout your analysis!
Step-by-Step Application Process
How to Apply KCL Systematically
Example Node Analysis
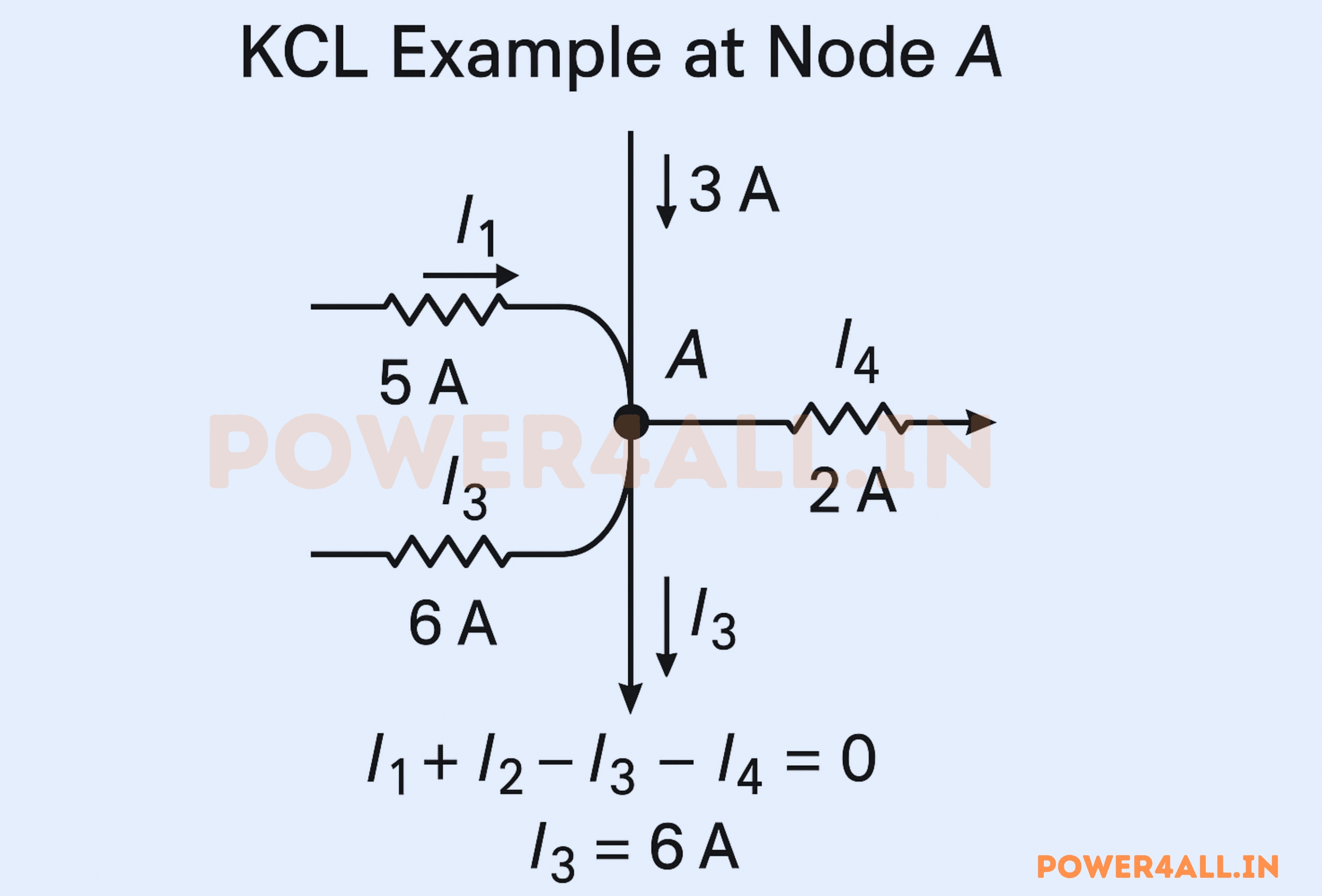
Node A Analysis:
Currents entering: I₁ = 5A, I₂ = 3A
Currents leaving: I₃ = ?, I₄ = 2A
KCL Application: I₁ + I₂ - I₃ - I₄ = 0
Solution: 5 + 3 - I₃ - 2 = 0 → I₃ = 6A
Practical Examples
Simple Three-Branch Node
Problem: Find the unknown current I₃
Given Information
- Current I₁ = 8A entering the node
- Current I₂ = 3A leaving the node
- Current I₃ = ? leaving the node
Solution Steps
Answer: I₃ = 5A leaving the node
Complex Multi-Node Circuit
Problem: Analyze a circuit with multiple unknown currents
Circuit Description
- Three nodes: A, B, and C
- Known: I₁ = 10A, I₆ = 4A
- Unknown: I₂, I₃, I₄, I₅
KCL Equations
- Node A: I₁ - I₂ - I₃ = 0
- Node B: I₂ + I₄ - I₅ = 0
- Node C: I₃ + I₅ - I₆ = 0
Note: This system requires additional information (like resistance values and Ohm's law) for complete solution.
Special Cases and Considerations
| Special Case | Description | KCL Application | Example |
|---|---|---|---|
| Two-terminal elements | Current in equals current out | Trivial application | Resistor, capacitor, inductor |
| Series connection | Same current through all elements | Current continuity | Christmas lights (old style) |
| Parallel branches | Current divides between paths | Standard KCL at junction | Home electrical outlets |
| Ground connections | Reference point (0V) | KCL still applies | Circuit common/ground |
Common Mistakes and How to Avoid Them
Avoid These Common Errors
- Inconsistent sign convention: Mixing positive/negative assignments
- Missing currents: Forgetting to include all branches at a node
- Wrong current direction: Misinterpreting assumed vs. actual current direction
- Unit confusion: Mixing mA, A, and μA in the same equation
- Dependent equations: Writing more equations than are independent
Physical Reality
KCL reflects the fact that electric charge is conserved - it cannot be created or destroyed at a circuit node.
Instantaneous Law
KCL applies at every instant in time, making it valid for both DC and AC circuit analysis.
Computer Analysis
All circuit simulators use KCL as a fundamental constraint when solving circuit equations.
Kirchhoff's Voltage Law (KVL) - Complete Guide
Kirchhoff's Voltage Law states that the algebraic sum of all voltages around any closed loop in a circuit equals zero. This law embodies the conservation of energy principle and provides the foundation for analyzing voltage distribution in electrical networks.
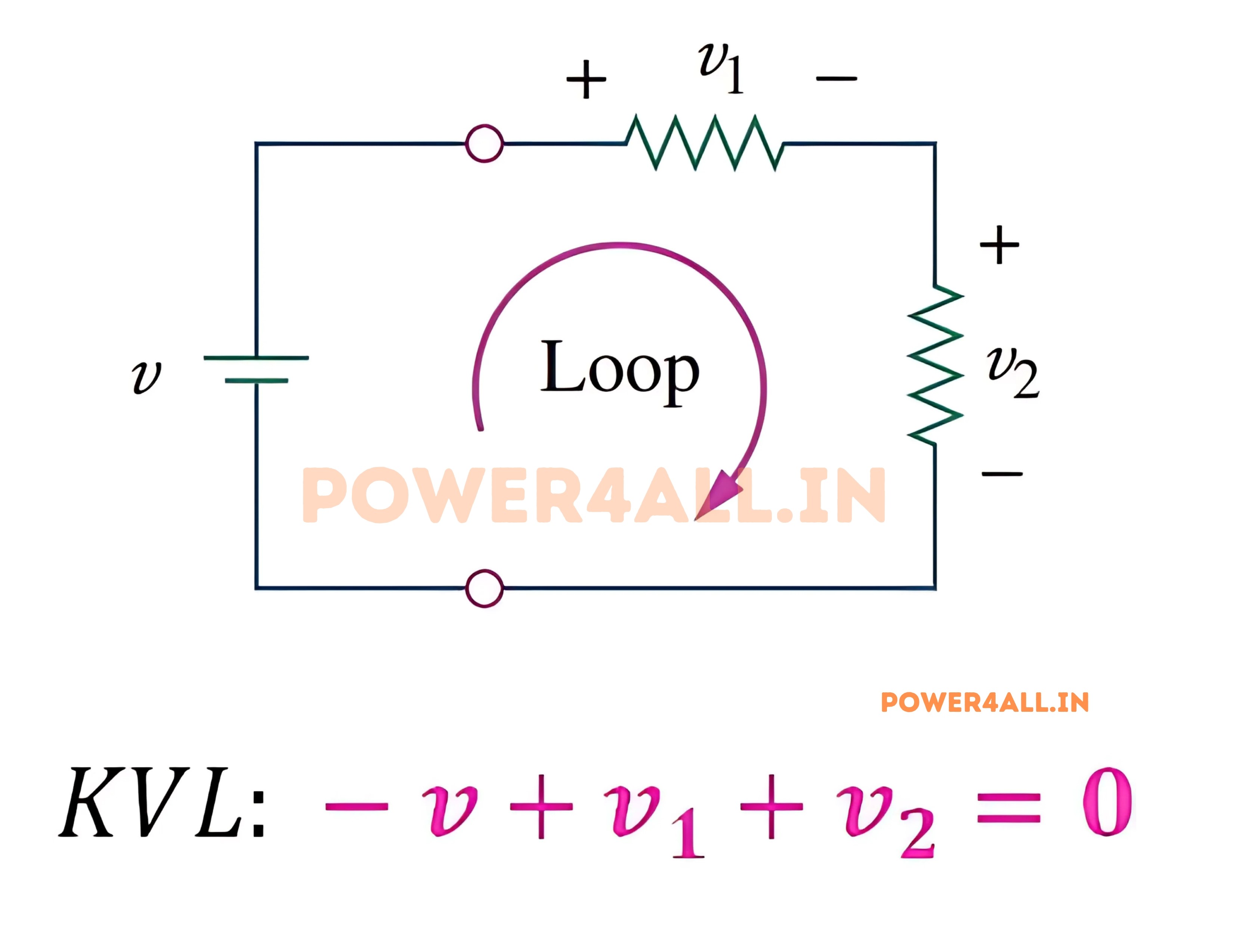
Mathematical Formulation
∑V = 0
Sum of all voltages around any closed loop
Alternative Forms
- ∑V_rises = ∑V_drops (Voltage rises = Voltage drops)
- V₁ + V₂ + V₃ + ... + Vₙ = 0 (Algebraic sum form)
- ∑V_sources = ∑V_loads (Energy balance form)
Voltage Polarity Convention
Two common approaches:
- Method 1: Voltage rises (+), Voltage drops (-)
- Method 2: Follow loop direction: same direction (+), opposite direction (-)
- Key: Consistency is crucial for correct results!
Understanding Voltage Rises and Drops
What Creates Voltage Rises and Drops?
Voltage Rises (Energy Sources)
Components that add energy to the circuit
Common Voltage Sources
- Batteries: Chemical energy → Electrical energy
- Generators: Mechanical energy → Electrical energy
- Solar cells: Light energy → Electrical energy
- Power supplies: AC → DC conversion
Battery Example
A 12V battery provides a 12V rise when you traverse from negative to positive terminal.
- (-) to (+): +12V rise
- (+) to (-): -12V drop
Voltage Drops (Energy Consumers)
Components that consume energy from the circuit
Common Voltage Drops
- Resistors: Electrical → Heat energy
- LEDs: Electrical → Light energy
- Motors: Electrical → Mechanical energy
- Speakers: Electrical → Sound energy
Resistor Example
A resistor with current flowing creates a voltage drop across it (V = IR).
- High to low potential: Voltage drop
- Energy dissipated as heat
Energy Balance Perspective
KVL ensures that all energy supplied by sources is exactly consumed by loads. No energy is lost or gained as you traverse a complete loop - it's the electrical equivalent of "what goes up must come down."
Step-by-Step KVL Application
Worked Examples
Simple Series Circuit
Find the voltage across the unknown resistor
Circuit: 24V battery + 10Ω resistor + R₂ (unknown) + 6Ω resistor
Given: Current I = 2A (same throughout series circuit)
Solution Steps
Error Analysis
Negative resistance is impossible! This indicates an error in our assumptions or calculations. Let's recalculate: V₂ = 24 - 20 - 12 = -8V suggests we made a sign error.
Corrected Solution
Proper KVL: +24 - 20 - V₂ - 12 = 0
Therefore: V₂ = 24 - 20 - 12 = -8V
This means our assumed polarity was wrong. The actual voltage drop is 8V.
Multi-Loop Circuit
Apply KVL to multiple loops simultaneously
Circuit: Two voltage sources, three resistors in a complex network
Given: V₁ = 12V, V₂ = 8V, R₁ = 4Ω, R₂ = 6Ω, R₃ = 3Ω
Loop Analysis
- Loop 1 (left): +12 - I₁×4 - I₃×3 = 0
- Loop 2 (right): +I₃×3 - I₂×6 + 8 = 0
- Plus KCL at center node: I₁ = I₂ + I₃
System of Equations
- 12 - 4I₁ - 3I₃ = 0
- 3I₃ - 6I₂ + 8 = 0
- I₁ - I₂ - I₃ = 0
Solution Method
This system can be solved using substitution, elimination, or matrix methods to find I₁, I₂, and I₃.
Practical Applications of KVL
| Application | How KVL is Used | Benefit | Real Example |
|---|---|---|---|
| Voltage Divider Circuits | Calculate output voltage from input | Create reference voltages | ADC voltage scaling |
| Battery Monitoring | Track voltage drops across cells | Prevent overcharge/discharge | Electric vehicle battery packs |
| Power Supply Design | Balance transformer windings | Optimal energy transfer | DC-DC converter design |
| LED String Design | Distribute voltage across LEDs | Uniform brightness control | Christmas light strings |
| Audio Amplifiers | Set bias points and gain | Optimal signal amplification | Transistor amplifier stages |
Sign Conventions and Best Practices
Consistent Loop Direction
Always traverse loops in the same direction (clockwise or counterclockwise) to maintain consistent sign conventions.
Polarity Awareness
Mark component polarities clearly before writing equations. Voltage sources and drops have specific polarities.
Verification Method
Always check that your KVL equation sums to zero. If not, review your sign conventions and polarity assignments.
Systematic Approach
Use a methodical approach: identify loops, assign directions, mark polarities, write equations, solve systematically.
Pro Tip
KVL is particularly powerful when combined with KCL in mesh analysis. This combination allows you to solve complex circuits with multiple loops and nodes systematically.
Practical Applications of Kirchhoff's Laws
Kirchhoff's Laws aren't just academic concepts - they're the foundation of virtually every electrical system around us. From the smartphone in your pocket to the power grid that lights your home, these laws enable engineers to design, analyze, and troubleshoot electrical systems reliably.
Consumer Electronics
Smartphone Circuits
Complex multi-voltage systems
KCL Applications
- Battery current distribution: Current splits between CPU, display, radio, and sensors
- Charging circuits: Current balancing in multi-cell batteries
- Power management: Dynamic current allocation based on usage
KVL Applications
- Voltage regulators: Step down from 3.7V battery to 1.8V, 1.2V, etc.
- Display backlighting: LED voltage drops in series/parallel combinations
- Audio amplifiers: Signal path voltage analysis
Real Example: Phone Charging
USB-C charging at 9V, 3A:
- Input: 9V × 3A = 27W from charger
- Conversion losses: ~2W in switching regulator
- Battery charging: 4.2V × 6A = 25.2W to battery
- KVL check: Input energy = Output energy + Losses ✓
Automotive Electronics
Safety-critical electrical systems
Engine Management
- Sensor networks: KCL for current distribution to oxygen sensors, temp sensors
- Injector control: KVL for precise voltage timing to fuel injectors
- Ignition system: High-voltage coil analysis using KVL
Safety Systems
- ABS braking: Wheel speed sensor current analysis
- Airbag deployment: Critical timing based on voltage/current calculations
- Battery management: 12V/48V system voltage monitoring
Safety Note
Automotive systems use Kirchhoff's Laws for fault detection. If measured currents don't match KCL predictions, the system knows there's a problem (short circuit, open wire, etc.)
Home Electrical Systems
Power distribution and safety
Circuit Breaker Design
- Load calculation: KCL determines total current on each circuit
- Voltage drop analysis: KVL ensures proper voltage at outlets
- Ground fault detection: KCL detects current imbalances
Smart Home Integration
- Energy monitoring: Smart meters use Kirchhoff's Laws for accurate measurement
- Solar panel systems: Grid-tie inverter design and analysis
- Electric vehicle charging: High-power charging station design
Household Circuit Example
Kitchen circuit with multiple appliances:
- Microwave: 1200W ÷ 120V = 10A
- Coffee maker: 800W ÷ 120V = 6.7A
- Toaster: 1500W ÷ 120V = 12.5A
- Total current (KCL): 10 + 6.7 + 12.5 = 29.2A
- Circuit breaker needed: 30A or 40A (never exceed 80% capacity)
Industrial and Power Systems
Large-Scale Electrical Systems
Power Generation and Distribution
Electrical Grid Management
Balancing supply and demand across vast networks
- Load flow analysis: KCL and KVL determine power flow through transmission lines
- Grid stability: Voltage regulation using transformer tap settings
- Fault analysis: Short circuit current calculations for protection
- Renewable integration: Solar and wind farm connection analysis
P_generated = P_consumed + P_losses
Power balance in electrical grids
Industrial Motor Control
Precise control of industrial machinery
- Variable frequency drives: Complex switching circuits analyzed with Kirchhoff's Laws
- Motor starting: Current rush limiting using reactance calculations
- Regenerative braking: Energy recovery system design
- Multi-motor coordination: Load sharing in parallel motor systems
Telecommunications Infrastructure
Modern communication systems rely heavily on Kirchhoff's Laws for signal integrity and power distribution:
| System | KCL Application | KVL Application | Critical Requirement |
|---|---|---|---|
| Cell Tower Power | Current distribution to amplifiers | Voltage regulation across temp ranges | 99.99% uptime requirement |
| Data Center UPS | Load balancing across servers | Battery backup voltage maintenance | Seamless power transfer |
| Fiber Optic Repeaters | Remote power over fiber analysis | Voltage drop over long cables | Signal regeneration accuracy |
| 5G Base Stations | Massive MIMO array power | RF amplifier bias networks | Precise phase relationships |
Circuit Analysis Methods Using Kirchhoff's Laws
Kirchhoff's Laws form the foundation of systematic circuit analysis methods. These techniques allow engineers to solve complex circuits with multiple sources, nodes, and loops by converting the physical circuit into a set of mathematical equations.
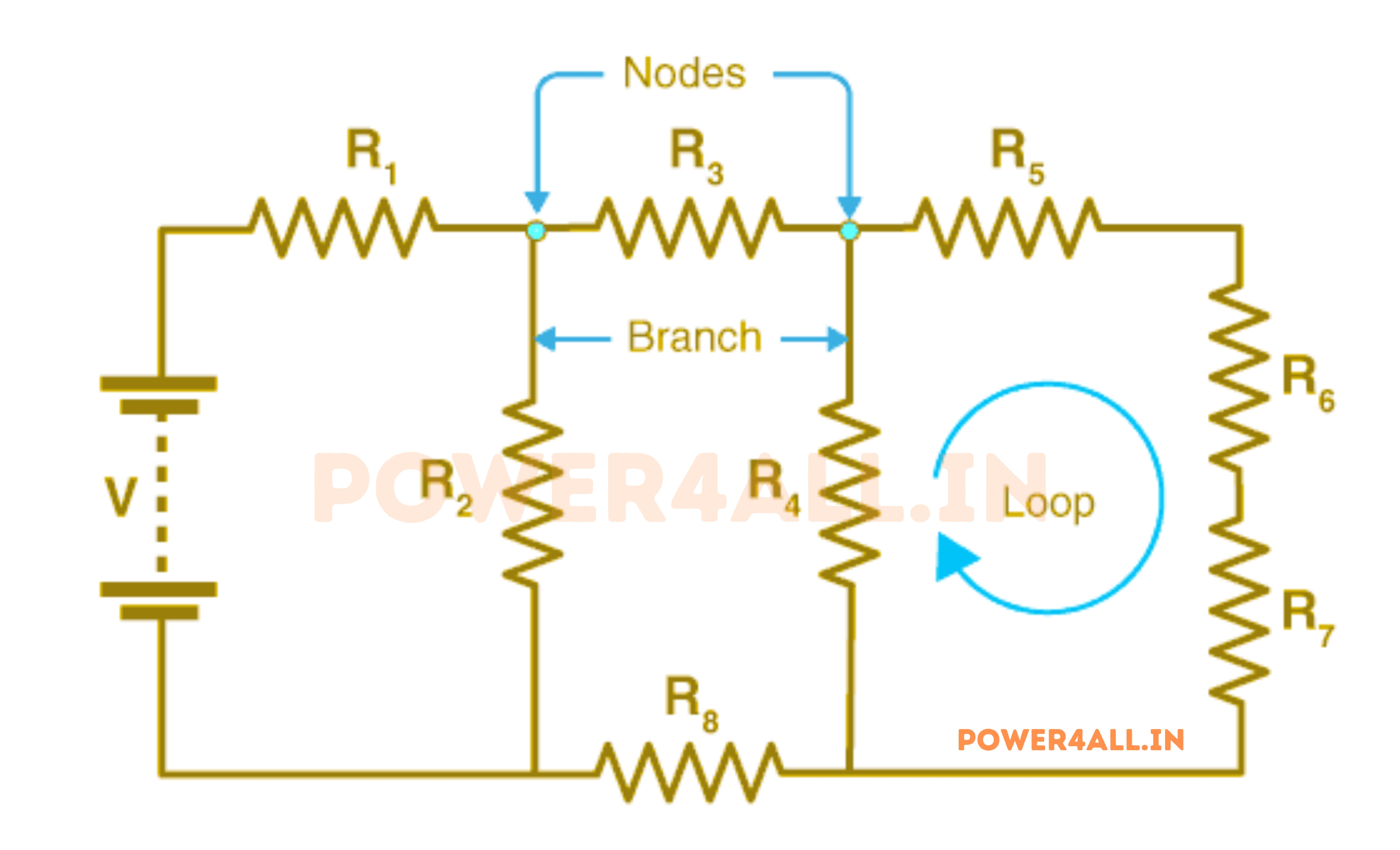
Node Voltage Analysis (Nodal Analysis)
Method Overview
Node voltage analysis uses KCL as the primary tool to solve circuits. We assign voltage variables to each node and write KCL equations based on currents flowing into and out of each node.
When to Use Nodal Analysis
- Fewer nodes than loops: More efficient than mesh analysis
- Current sources present: Easily handled in nodal analysis
- Need node voltages: Direct solution for voltage values
- Computer analysis: Easier to program and automate
Nodal Analysis Steps
Detailed Nodal Analysis Example
Example Circuit
Circuit Description: Two voltage sources (15V, 25V), three resistors (50Ω, 25Ω, 30Ω), find all node voltages and branch currents.
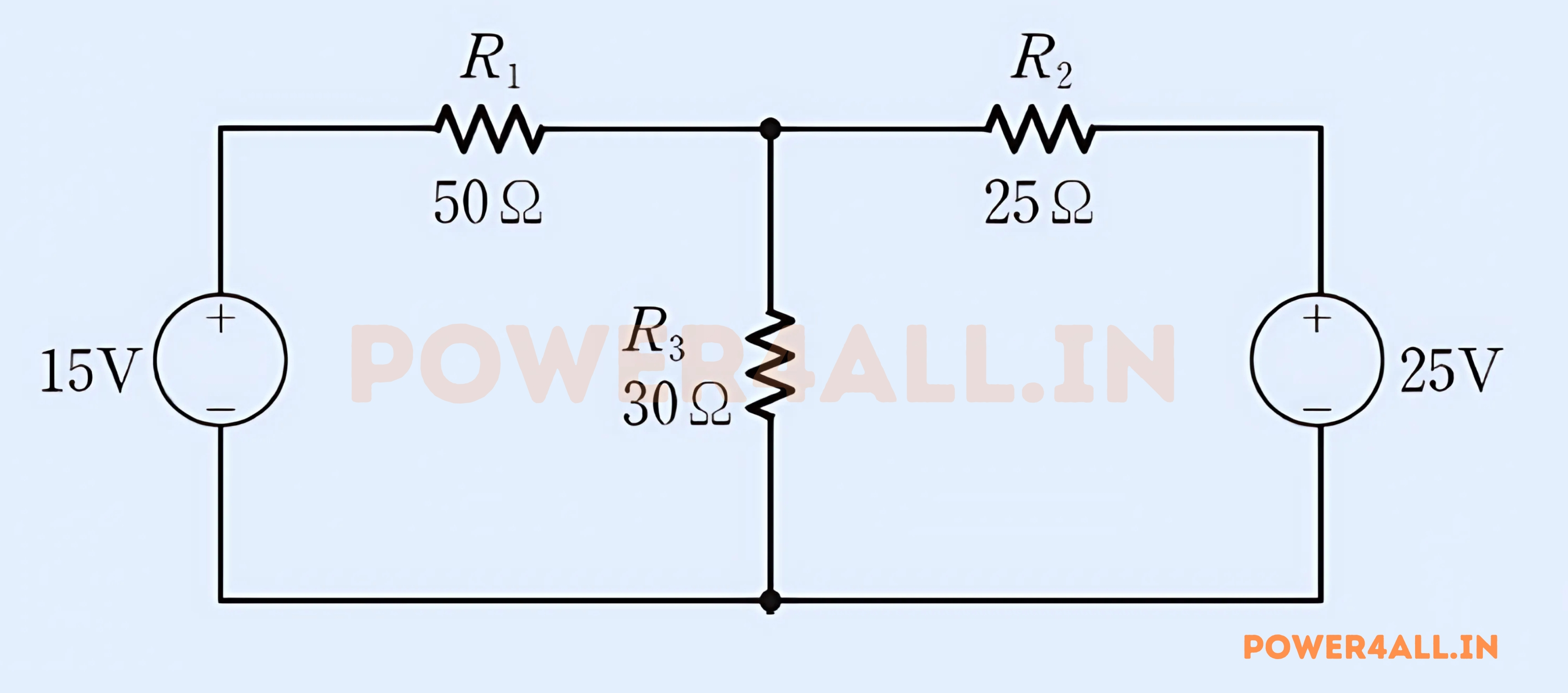
Choose bottom node as ground (0V reference)
Middle node: V₁
At node 1: (15-V₁)/50 + V₁/30 + (V₁-25)/25 = 0
Node 1: 0.3 - 0.02V₁ + 0.033V₁ + 0.04V₁ - 1 = 0
Equation 1: 0.053V₁ = 0.7
V₁ = 13.21V
V₁ = 13.21V
Verification
Always verify your solution by substituting back into the original KCL equations and checking that currents sum to zero at each node.
Mesh Current Analysis (Loop Analysis)
Method Overview
Mesh analysis uses KVL as the primary tool to solve circuits. We assign current variables to each mesh (loop) and write KVL equations for the voltage drops around each loop.
When to Use Mesh Analysis
- Fewer loops than nodes: More efficient than nodal analysis
- Voltage sources present: Directly incorporated in mesh equations
- Need loop currents: Direct solution for current values
- Planar circuits: Works best with circuits that can be drawn without crossing wires
Mesh Analysis Steps
Comparison of Analysis Methods
| Aspect | Nodal Analysis | Mesh Analysis | Best Choice |
|---|---|---|---|
| Primary Law Used | KCL (current conservation) | KVL (voltage conservation) | Depends on circuit structure |
| Variables Solved | Node voltages | Loop currents | Choose based on what you need |
| Number of Equations | Number of nodes - 1 | Number of independent loops | Use method with fewer equations |
| Current Sources | Easy to handle | Requires special treatment | Nodal for circuits with current sources |
| Voltage Sources | Requires special treatment | Easy to handle | Mesh for circuits with voltage sources |
| Computer Implementation | More systematic, easier to program | Less systematic structure | Nodal preferred for SPICE-type simulators |
Advanced Techniques
Superposition Method
For circuits with multiple sources, analyze one source at a time (others zeroed) and sum the results.
Thevenin/Norton Equivalents
Simplify complex networks to single source and resistor equivalents for easier analysis.
Computer-Aided Analysis
Software like SPICE uses modified nodal analysis for automatic circuit simulation.
AC Analysis Extension
Same methods apply to AC circuits using complex impedances instead of resistances.
Worked Examples: Step-by-Step Solutions
Let's work through comprehensive examples that demonstrate how to apply Kirchhoff's Laws to solve real circuits. These examples progress from simple to complex, showing different techniques and common scenarios you'll encounter in practice.
Example 1: Simple Series-Parallel Circuit
Problem Statement
Find the current through each resistor and the voltage across each component in the circuit shown below.
Given:
- Voltage source: V₁ = 24V
- Resistors: R₁ = 6Ω, R₂ = 4Ω, R₃ = 12Ω
- R₂ and R₃ are in parallel, then in series with R₁
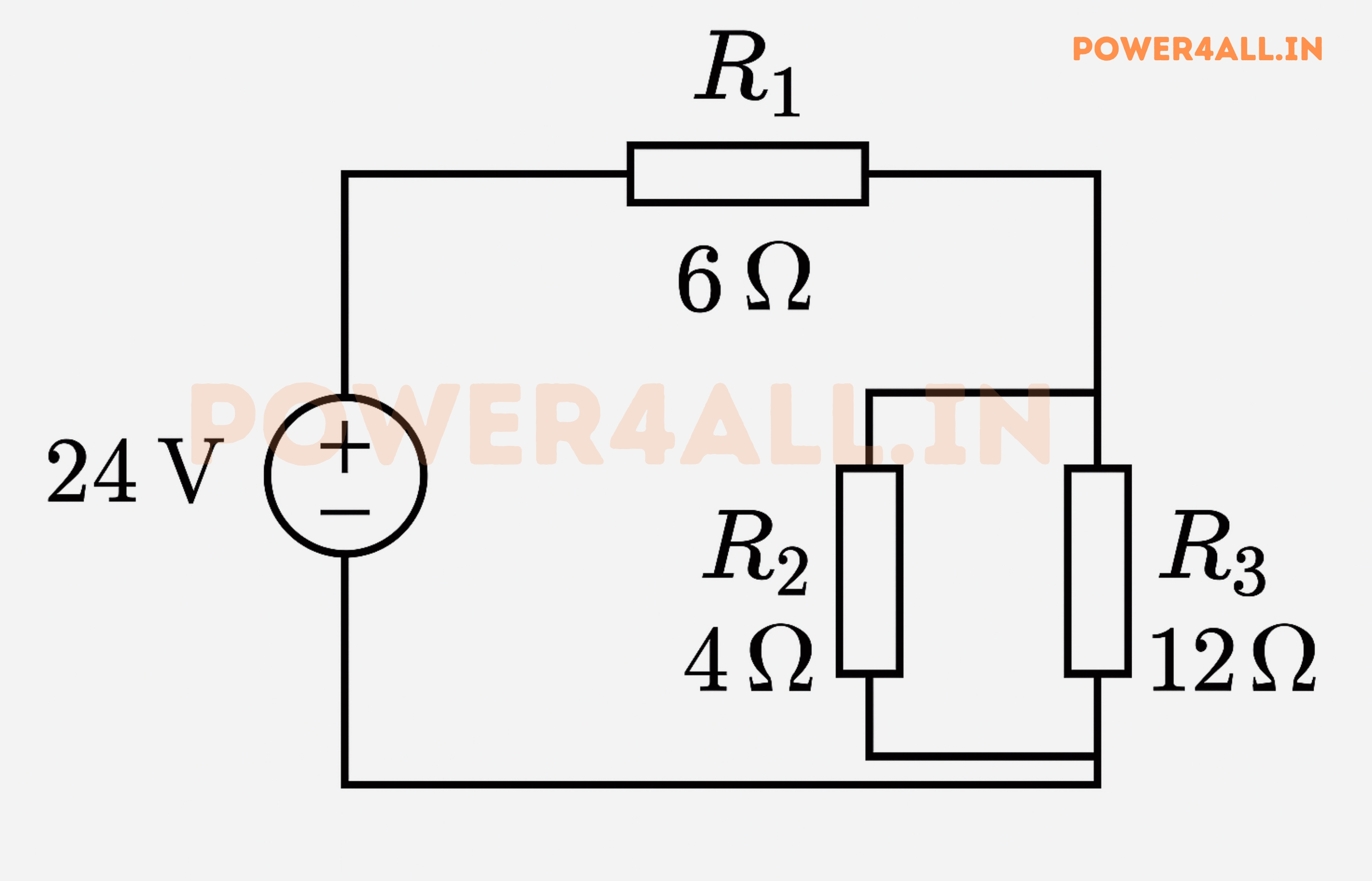
Solution Method
R₂₃ = (R₂ × R₃)/(R₂ + R₃) = (4 × 12)/(4 + 12) = 48/16 = 3Ω
R_total = R₁ + R₂₃ = 6 + 3 = 9Ω
I_total = V₁/R_total = 24V/9Ω = 2.67A
V_R₁ = I_total × R₁ = 2.67A × 6Ω = 16V
V_R₂₃ = V₁ - V_R₁ = 24V - 16V = 8V
I_R₂ = V_R₂₃/R₂ = 8V/4Ω = 2A
I_R₃ = V_R₂₃/R₃ = 8V/12Ω = 0.67A
Verification Using KCL
At the parallel junction:
Current entering = I_total = 2.67A
Current leaving = I_R₂ + I_R₃ = 2A + 0.67A = 2.67A ✓
KCL is satisfied!
Verification Using KVL
Around the complete loop:
+24V - 16V - 8V = 0 ✓
KVL is satisfied!
Advanced Applications of Kirchhoff's Laws
Beyond basic circuit analysis, Kirchhoff's Laws enable sophisticated applications in modern technology. From AC power systems to digital circuit design, these fundamental principles adapt to complex, real-world engineering challenges.
AC Circuit Analysis
Phasor Domain Application
In AC circuits, Kirchhoff's Laws work with complex numbers (phasors) to handle magnitude and phase relationships. This enables analysis of power systems, motors, and communication circuits.
∑V̄ = 0, ∑Ī = 0
KVL and KCL with complex phasors
AC Power System Example
Three-phase power distribution:
- Voltage sources: 120V∠0°, 120V∠-120°, 120V∠+120°
- Load balancing: KCL ensures equal current distribution
- Neutral current: Sum of three phases = 0 (ideally)
- Power factor: Phase relationships determine efficiency
Frequency Domain Analysis
Filter Design
Active and passive filters for signal processing
Low-Pass Filter Analysis
- RC network: Voltage divider with frequency-dependent impedance
- Transfer function: H(jω) = 1/(1 + jωRC)
- Cutoff frequency: fc = 1/(2πRC)
- Phase response: φ(ω) = -arctan(ωRC)
H(jω) = Vout/Vin
Frequency response using KVL
Resonant Circuits
LC oscillators and tuned amplifiers
Series RLC Resonance
- Resonant frequency: fr = 1/(2π√LC)
- Impedance minimum: Z = R at resonance
- Quality factor: Q = ωL/R = 1/(ωRC)
- Bandwidth: BW = fr/Q
FM Radio Tuner Example
88-108 MHz band selection:
- Variable capacitor adjusts resonant frequency
- High Q provides selectivity
- KVL determines voltage gain at resonance
Switching Circuits
Power converters and digital systems
Buck Converter Analysis
- Switch ON: Inductor stores energy from input
- Switch OFF: Inductor releases energy to load
- Continuous mode: IL never reaches zero
- Voltage conversion: Vout = D × Vin (D = duty cycle)
State-Space Analysis
Modern switching converter design uses state-space averaging to apply Kirchhoff's Laws to time-varying circuits.
Digital Circuit Applications
Logic Gates and Signal Integrity
Power Distribution Networks (PDN)
Modern microprocessors require extremely stable power delivery with minimal voltage ripple. Kirchhoff's Laws help design the complex PDN that feeds power to millions of transistors.
| Component | KCL Application | KVL Application | Design Challenge |
|---|---|---|---|
| VRM (Voltage Regulator Module) | Current sensing and feedback | Output voltage regulation | Sub-millivolt accuracy |
| Decoupling Capacitors | Transient current supply | Voltage ripple minimization | High-frequency effectiveness |
| Power Planes | Current distribution paths | Resistance and inductance minimization | Electromagnetic compatibility |
| Via Arrays | Layer-to-layer current flow | Voltage drop across PCB layers | Thermal management |
Signal Integrity Analysis
High-speed digital signals require transmission line analysis where Kirchhoff's Laws combine with electromagnetic theory.
Characteristic Impedance
Z₀ = √(L/C) where L and C are per-unit-length inductance and capacitance, derived from field theory and confirmed by circuit analysis.
Reflection Analysis
Voltage reflections at impedance discontinuities analyzed using KVL and transmission line equations.
Crosstalk Modeling
Mutual inductance and capacitance between traces create coupled circuits analyzed with extended Kirchhoff's Laws.
Renewable Energy Systems
Solar Panel Array Design
Optimizing power harvest and system reliability
String Configuration Analysis
Solar panels can be connected in series (strings) and parallel (arrays). Kirchhoff's Laws determine optimal configurations for maximum power and fault tolerance.
Real System Example
Residential 10kW solar system:
- Panel specs: 400W, 40V, 10A per panel
- String configuration: 10 panels in series = 400V, 10A
- Array configuration: 2.5 strings in parallel = 400V, 25A
- Inverter input: 400V DC → 240V AC conversion
Safety Considerations
High-voltage DC systems require special safety procedures. Series-connected solar panels can generate lethal voltages even in low light conditions.
Problem Solving Techniques
Mastering Kirchhoff's Laws requires systematic problem-solving approaches. This section provides step-by-step methodologies, common troubleshooting techniques, and strategies for tackling complex circuit analysis problems efficiently and accurately.
General Problem-Solving Strategy
The UNDERSTAND Method
A systematic approach to tackle any circuit analysis problem:
Quick Decision Tree
Which analysis method to choose?
Use Nodal Analysis When:
- Fewer nodes than meshes
- Current sources present
- Need node voltages
- Computer analysis planned
Use Mesh Analysis When:
- Fewer meshes than nodes
- Only voltage sources
- Need loop currents
- Planar circuit topology
Use Source Transformation When:
- Mixed sources complicate analysis
- Simplification possible
- Series/parallel combinations
Common Problem Types and Approaches
Find Unknown Currents
Most common circuit analysis problem
Strategy
- Step 1: Assign current directions to all branches
- Step 2: Apply KCL at all but one node
- Step 3: Use Ohm's Law to relate voltages to currents
- Step 4: Solve the system of equations
- Step 5: Interpret negative results as opposite direction
Pro Tip
If you get a negative current, don't start over! The magnitude is correct; just the direction is opposite to your assumption.
Find Unknown Voltages
Voltage analysis and distribution problems
Strategy
- Step 1: Select ground reference node
- Step 2: Assign voltage variables to remaining nodes
- Step 3: Express branch currents in terms of node voltages
- Step 4: Apply KCL at each node
- Step 5: Solve for node voltages
Voltage Divider Insight
Many voltage problems can be simplified by recognizing voltage divider patterns:
Vout = Vin × R2/(R1+R2)
Find Unknown Component Values
Design and reverse-engineering problems
Strategy
- Step 1: Use given operating conditions as constraints
- Step 2: Set up equations with unknown as variable
- Step 3: Apply Kirchhoff's Laws to relate unknowns to knowns
- Step 4: Solve for unknown component value
- Step 5: Check if result is physically reasonable
Reality Check
Always verify that calculated component values are commercially available and within reasonable ranges for the application.
Advanced Problem-Solving Techniques
Sophisticated Analysis Methods
Superposition Principle
For linear circuits with multiple sources, analyze one source at a time with others turned off (voltage sources shorted, current sources opened).
Thevenin and Norton Equivalent Circuits
Simplify complex networks to single source and impedance for easier analysis of load effects.
Thevenin Equivalent
Steps to Find Thevenin Equivalent
- Vth: Open-circuit voltage at load terminals
- Rth: Resistance seen from terminals with sources zeroed
- Result: Voltage source Vth in series with Rth
Norton Equivalent
Steps to Find Norton Equivalent
- In: Short-circuit current at load terminals
- Rn: Same as Rth (resistance with sources zeroed)
- Result: Current source In in parallel with Rn
Source Transformation
Convert between voltage and current source representations to simplify analysis.
Vs = Is × Rs, Is = Vs / Rs
Voltage source ↔ Current source conversion
Troubleshooting Circuit Problems
| Problem Symptom | Likely Cause | KCL/KVL Check | Solution Approach |
|---|---|---|---|
| No current flow | Open circuit | KCL: Current into node ≠ current out | Check continuity, find break |
| Excessive current | Short circuit | KVL: Voltage drops don't sum to source | Look for unintended connections |
| Wrong voltage levels | Incorrect component values | Both laws may be satisfied but wrong operating point | Verify component values and calculations |
| Oscillation or instability | Positive feedback | Time-varying behavior violates steady-state analysis | Check for unintended feedback paths |
Common Mistakes and How to Avoid Them
Sign Convention Errors
Problem: Inconsistent positive/negative assignments
Solution: Establish clear convention and stick to it throughout
Missing Equations
Problem: Not writing enough independent equations
Solution: Count unknowns and ensure equal number of independent equations
Unit Errors
Problem: Mixing different units (mA vs A, kΩ vs Ω)
Solution: Convert all values to consistent units before calculating
Dependent Sources
Problem: Treating dependent sources like independent ones
Solution: Express dependent source in terms of controlling variable
Success Tips
- Start simple: Practice with basic circuits before tackling complex problems
- Draw clearly: Neat, labeled diagrams prevent errors
- Check units: Dimensional analysis catches many mistakes
- Verify results: Use multiple methods to confirm answers
- Practice regularly: Problem-solving skills improve with repetition
Frequently Asked Questions About BJTs
Common questions about BJT transistors, their operation, applications, and troubleshooting. These answers address the most frequent concerns from students, hobbyists, and engineers working with BJT technology.
Basic Operation and Theory
Q: What's the difference between KCL and KVL, and when do I use each?
Ans: KCL (Current Law) deals with current conservation at nodes/junctions, while KVL (Voltage Law) deals with energy conservation around closed loops.
- Use KCL when: You need to find unknown currents, analyze current distribution, or apply nodal analysis
- Use KVL when: You need to find unknown voltages, analyze voltage drops, or apply mesh analysis
- Use both when: Solving complex circuits with multiple unknowns
In practice, most circuit analysis uses both laws together to create a complete system of equations.
Q: Why do I get negative values when solving circuit problems? Did I make a mistake?
Ans: Negative values are often correct! They simply mean your assumed direction was opposite to the actual direction.
- Negative current: Current flows opposite to your assumed arrow direction
- Negative voltage: Polarity is opposite to your assumed + and - markings
- What to do: Keep the magnitude, but understand the actual direction is reversed
Example: If you calculate I = -2A, the actual current is 2A flowing in the opposite direction to your assumption. This is completely valid and correct.
Q: Do Kirchhoff's Laws work for AC circuits with different frequencies?
Ans: Yes, but with important modifications:
- Use complex phasors: Voltages and currents become complex numbers with magnitude and phase
- Impedance replaces resistance: Z = R + jX where X includes reactive components
- Instantaneous form: Laws apply at every instant in time
- RMS/phasor form: Laws apply to RMS values and phasor relationships
Frequency limitations: At very high frequencies (GHz range), distributed effects and electromagnetic wave propagation must be considered, requiring more advanced analysis methods.
Q: How do dependent sources affect Kirchhoff's Laws analysis?
Ans: Dependent sources require special treatment:
- Apply KCL and KVL normally: Dependent sources still follow the fundamental laws
- Express the dependency: Write the dependent source value in terms of the controlling variable
- Solve the system: Include the dependency relationship as an additional constraint
Example: Current-controlled voltage source (CCVS) with gain k:
- Vs = k × Icontrol (dependency relationship)
- Apply KVL: V1 + Vs + V2 = 0
- Substitute: V1 + k×Icontrol + V2 = 0
- Express Icontrol in terms of other circuit variables
Q: What happens to Kirchhoff's Laws in nonlinear circuits with diodes and transistors?
Ans:Kirchhoff's Laws still apply, but solution methods change:
- Laws remain valid: Current and voltage conservation still hold
- Linear relationships break: Ohm's Law doesn't apply to nonlinear elements
- Iterative solutions: Use Newton-Raphson or other numerical methods
- Approximation methods: Piecewise linear models, small-signal analysis
Practical approaches:
- Diode circuits: Assume forward voltage drop (0.7V for silicon)
- Transistor circuits: Use appropriate models (Ebers-Moll, small-signal)
- SPICE simulation: Computer tools handle the nonlinear math automatically
Q: How many equations do I need to solve a circuit completely?
Ans: Number of equations must equal number of unknowns:
- Count unknowns: Unknown currents, voltages, or component values
- Independent KCL equations: Number of nodes - 1
- Independent KVL equations: Number of independent loops
- Component relationships: Ohm's Law for each resistor
General formula for networks:
- Total equations needed: Number of branches (currents to find)
- KCL equations: n - 1 (where n = number of nodes)
- KVL equations: b - n + 1 (where b = number of branches)
Tip: If you have more equations than unknowns, some equations are dependent (redundant).
Q: Can I use Kirchhoff's Laws for circuits with transformers and mutual inductance?
Ans: Yes, with modifications for magnetic coupling:
- Basic laws apply: Current and voltage conservation remain valid
- Mutual inductance: Creates voltage coupling between separate loops
- Modified KVL: Include mutually induced voltages in loop equations
Transformer analysis:
- Primary side: V1 = L1(di1/dt) + M(di2/dt)
- Secondary side: V2 = L2(di2/dt) + M(di1/dt)
- Ideal transformer: V2/V1 = N2/N1, I1/I2 = N2/N1
Practical approach: Use equivalent circuit models or ideal transformer relationships to simplify analysis.
Q: Why don't my calculated values match my measured values exactly?
Ans: Real-world factors cause differences between theory and practice:
Component Tolerances
- Resistor tolerance: ±1%, ±5%, ±10% typical variations
- Capacitor tolerance: ±10%, ±20% common
- Component aging: Values drift over time
Measurement Limitations
- Meter accuracy: ±1% typical for handheld meters
- Loading effects: Meter resistance affects circuit
- Temperature effects: Component values change with temperature
Parasitic Effects
- Wire resistance: Especially significant in high-current circuits
- Contact resistance: Connection points add resistance
- Stray capacitance and inductance: Affects high-frequency behavior
Typical agreement: Within 5-10% is excellent for hand calculations vs. measurements.
Conclusion: Mastering Kirchhoff's Laws
Kirchhoff's Laws are more than just academic concepts - they're the fundamental principles that govern every electrical system around us. From the simple flashlight to complex power grids, these laws provide the mathematical foundation for understanding, analyzing, and designing electrical circuits.
Key Takeaways
Universal Principles
KCL and KVL are based on fundamental conservation laws (charge and energy) that apply to all electrical circuits, regardless of complexity.
Practical Tools
These laws provide systematic methods for solving any circuit problem, from simple series resistors to complex multi-source networks.
Modern Relevance
Every circuit simulator, from SPICE to modern CAD tools, uses Kirchhoff's Laws as their computational foundation.
Design Foundation
Understanding these laws enables you to design circuits that work reliably and efficiently in real-world applications.
Congratulations!
You've completed a comprehensive journey through Kirchhoff's Laws. You now have the foundation to tackle any circuit analysis problem and understand the electrical systems that power our modern world. Keep practicing, keep learning, and most importantly, keep building!